【题目】如图,点E,F分别在x轴,y轴的正半轴上.点![]() 在线段EF上,过A作
在线段EF上,过A作![]() 分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作
分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作![]() ,交CP的延长线于点G,交CA的延长线于点D.有以下结论①
,交CP的延长线于点G,交CA的延长线于点D.有以下结论①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的结论是_____.(写出所有正确结论的番号)
,其中正确的结论是_____.(写出所有正确结论的番号)

参考答案:
【答案】①③④.
【解析】
如图,作AM⊥y轴于M,AN⊥OE于N.首先证明四边形AMON是正方形,再证明△AMF≌△ANB(ASA),△AMC≌△ANE(ASA),△AFC≌△ABE(SSS)即可解决问题.
解:如图,作AM⊥y轴于M,AN⊥OE于N.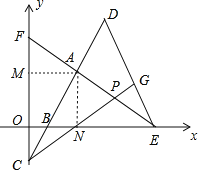
∵A(4,4),
∴AM=AN=4,
∵∠AMO=∠ONA=90°,
∴四边形ANON是矩形,
∵AM=AN,
∴四边形AMON是正方形,
∴OM=ON=4,
∴∠MAN=90°,
∵CD⊥EF,
∴∠FAC=∠MAN=90°,
∴△AMF≌△ANB(ASA),∴FM=BN,
∴OF+OB=OM+FM+ON-BN=2OM=8,故③正确,
同法可证△AMC≌△ANE(ASA),
∴CM=NE,AC=AE,故①正确;
∵FM=BN,
∴CF=BE,
∵AC=AE,AF=AB,
∴△AFC≌△ABE(SSS),
∴S△ABE-S△BOC=S△AFC-S△BOC=S四边形ABOF=S正方形AMON=16,故④正确,
当BE为定值时,点P是动点,故PC≠BE,故②错误,
故答案为①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
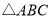 中,
中,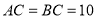 ,
,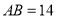 ,将
,将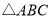 绕点A按顺时针方向旋转得到
绕点A按顺时针方向旋转得到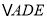 旋转角为
旋转角为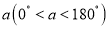 ,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当
,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当 时,点P与点C之间的距离是________.
时,点P与点C之间的距离是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】每年“双十一”购物活动,商家都会利用这个契机进行打折满减的促销活动.某商家平时的优惠措施是按所有商品标价打七折:“双十一”活动期间的优惠措施是:购买的所有商品先按标价总和打七五折,再享受折后每满
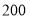 元减
元减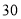 元的优惠.如标价为
元的优惠.如标价为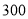 元的商品,折后为
元的商品,折后为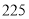 元,再减
元,再减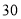 元,即实付:
元,即实付: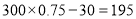 (元).
(元).(1)该商店标价总和为
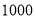 元的商品,在“双十一”购买,最后实际支付只需多少元?
元的商品,在“双十一”购买,最后实际支付只需多少元?(2)小明妈妈在这次活动中打算购买某件商品,打折满减后,应付金额是
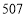 元,求该商品的标价.
元,求该商品的标价.(3)在(2)的条件下,若该商家出售的商品标价均为整数,小明通过计算后告诉妈妈:通过凑单(再购买少量商品)实际支付金额只需再多付 元,就可获得最大优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】[阅读理解]射线
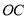 是
是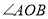 内部的一条射线,若
内部的一条射线,若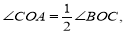 则我们称射线
则我们称射线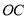 是射线
是射线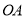 的伴随线.
的伴随线.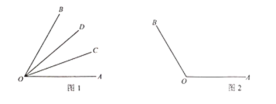
例如,如图1,
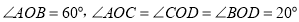 ,则
,则 ,称射线
,称射线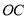 是射线
是射线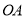 的伴随线:同时,由于
的伴随线:同时,由于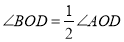 ,称射线
,称射线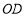 是射线
是射线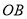 的伴随线.
的伴随线.[知识运用]
(1)如图2,
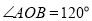 ,射线
,射线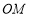 是射线
是射线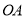 的伴随线,则
的伴随线,则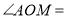 ,若
,若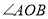 的度数是
的度数是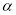 ,射线
,射线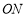 是射线
是射线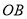 的伴随线,射线
的伴随线,射线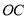 是
是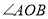 的平分线,则
的平分线,则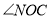 的度数是 .(用含
的度数是 .(用含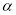 的代数式表示)
的代数式表示)(2)如图,如
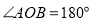 ,射线
,射线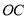 与射线
与射线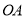 重合,并绕点
重合,并绕点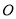 以每秒
以每秒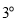 的速度逆时针旋转,射线
的速度逆时针旋转,射线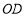 与射线
与射线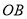 重合,并绕点
重合,并绕点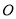 以每秒
以每秒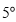 的速度顺时针旋转,当射线
的速度顺时针旋转,当射线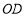 与射线
与射线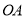 重合时,运动停止,现在两射线同时开始旋转.
重合时,运动停止,现在两射线同时开始旋转.
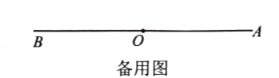
①是否存在某个时刻
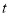 (秒),使得
(秒),使得 的度数是
的度数是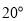 ,若存在,求出
,若存在,求出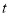 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;②当
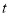 为多少秒时,射线
为多少秒时,射线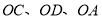 中恰好有一条射线是其余两条射线的伴随线.
中恰好有一条射线是其余两条射线的伴随线. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=
 .
.(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
 +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式. -
科目: 来源: 题型:
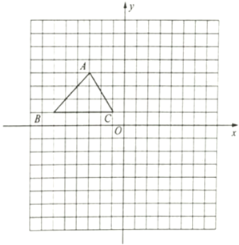
查看答案和解析>>【题目】如图,已知
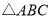 的三个顶点的坐标分别为
的三个顶点的坐标分别为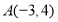 ,
,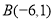 ,
,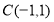 .
.
(1)画出
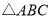 关于原点中心对称的
关于原点中心对称的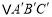 ,其中A,B,C的对应点分别为
,其中A,B,C的对应点分别为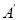 ,
,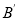 ,
,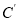 ;
;(2)在(1)的基础上,将
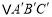 向上平移4个单位长度,画出平移后的
向上平移4个单位长度,画出平移后的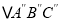 ,并写出
,并写出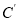 的对应点
的对应点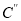 的坐标;
的坐标;(3)D为y轴上一点,且
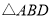 是以AB为直角边的直角三角形.请直接写出D点的坐标.
是以AB为直角边的直角三角形.请直接写出D点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC=3,直线l是抛物线的对称轴,E是抛物线的顶点.
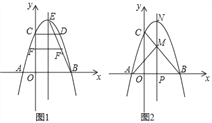
(I)求b,c的值;
(Ⅱ)如图1,连BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(Ⅲ)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
相关试题

