【题目】如图,己知OA丄OB, ∠AOC=∠BOD,由此判定OC丄OD,下面是推理过程,请在横线上填空.
![]() OA丄OB(己知)
OA丄OB(己知)
![]() _________=90° (______________)
_________=90° (______________)
![]() ∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC
∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC
∠AOC=∠BOD
![]() ∠AOB=∠COD (等式的性质)
∠AOB=∠COD (等式的性质)
![]() _________=90°
_________=90°
![]() CO 丄 OD (_____________________)
CO 丄 OD (_____________________)

参考答案:
【答案】见解析
【解析】试题分析:由OA丄OB,根据垂直的定义得到∠AOB=90°,由图可得∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC和已知∠AOC=∠BOD,根据等式的性质可得∠AOB=∠COD,再根据等量代换可得∠COD=90°,再根据垂直的定义可得CO 丄 OD.
试题解析:
![]() OA丄OB(己知)
OA丄OB(己知)
![]() ∠AOB =90° (垂直的定义)
∠AOB =90° (垂直的定义)
![]() ∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC,∠AOC=∠BOD
∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC,∠AOC=∠BOD
![]() ∠AOB=∠COD (等式的性质)
∠AOB=∠COD (等式的性质)
![]() ∠COD =90°
∠COD =90°
![]() CO 丄 OD (垂直的定义).
CO 丄 OD (垂直的定义).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=
 CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.(1)求证:AB=BG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的有()
(1) 钝角的补角一定是锐角
(2) 过己知直线外一点作这条直线的垂线有且只有一条
(3) —个角的两个邻补角是对顶角
(4) 等角的补角相等
(5) 直线
 外一点A与直线
外一点A与直线 上各点连接而成的所有线段中,最短线段的长是3cm,则
上各点连接而成的所有线段中,最短线段的长是3cm,则点A到直线
 的距离是3cm .
的距离是3cm .A. 2个 B. 3个 C. 4 个 D. 5 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=1,BC=
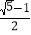 ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,点C(1,n)在直线AB上,点D在y轴的负半轴上,且CD=
 .
.(1)求点C、点D的坐标.
(2)若P为y轴上的点,当△PCD为等腰三角形时,求点P的坐标.
(3)若点M为x轴上一动点(点M不与点O重合),N为直线y=2x-5上一动点,是否存在点M、N,使得△AMN与△AOB全等?若存在,求出点N的坐标;若不存在,请说明理由.


图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,已知AC=3,BC=4.

(1)线段AD,CD,CD,BD是不是成比例线段?写出你的理由;
(2)在这个图形中,能否再找出其他成比例的四条线段?如果能,请至少写出两组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】补全下列各题解题过程.
如图,EF∥AD,∠1 = ∠2,∠BAC = 70°,求 ∠AGD 的度数.

解:∵EF∥AD ( 已知 )
∴∠2 = ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AB∥ ( )
∴∠BAC + = 180°( )
∵∠BAC = 70°(已知 )
∴∠AGD = _ .
相关试题

