【题目】(阅读理解):A,B,C为数轴上三点,若点C到A的距离CA是点C到B的距离CB的2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离CA是2,到点B的距离CB是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离DA是1,到点B的距离DB是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
(知识运用):(1)如图1,表示数______和_______的点是(A,B)的好点;

(2)如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

①表示数______的点是(M,N)的好点;
②表示数______的点是(N,M)的好点;
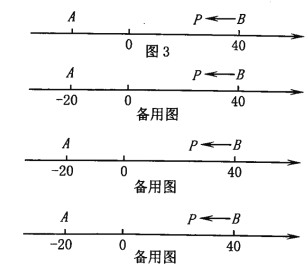
(3)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动.当t为何值时,P、A和B中恰有一个点为其余两点的好点?
参考答案:
【答案】(1)1;5;(2)①2或10;②0或![]() ;(3)当t为10秒或15秒或20秒或50秒或60秒或80秒时,P、A和B中恰有一个点为其余两点的好点.
;(3)当t为10秒或15秒或20秒或50秒或60秒或80秒时,P、A和B中恰有一个点为其余两点的好点.
【解析】
(1)设所求数为x,可分为:①当好点在A、B之间;②当好点在B点右边,根据好点的定义,列出方程,解方程即可;
(2)①与(1)同理,可分为好点在M、N之间和N的右边,两种情况进行计算即可;
②与(1)同理,可分为好点在M、N之间和点M的左边,两种情况进行计算即可;
(3)根据好点的定义可知分五种情况:①P为(A,B)的好点;②P为(B,A)的好点;③点B是(A、P)的好点;④点A是(B,P)的好点;⑤点A是(P,B)的好点;设点P表示的数为n,根据好点的定义列出方程,进而得出t的值.
解:(1)设所求数为x,则
①当好点在A、B之间时,有:![]() ,解得:
,解得:![]() ;
;
②当好点在B的右边时,有:![]() ,解得:
,解得:![]() ;
;
∴表示数1和数5的点是(A,B)的好点;
故答案为:1;5.
(2)①设所求数为y,则
当好点在M、N之间时,有:![]() ,解得:
,解得:![]() ;
;
当好点在N的右边时,有:![]() ,解得:
,解得:![]() ;
;
∴表示数2或10的点是(M,N)的好点;
故答案为:2或10;
②设所求数为z,则
当好点在M、N之间时,有:![]() ,解得:
,解得:![]() ;
;
当好点在M的左边时,有:![]() ,解得:
,解得:![]() ;
;
∴表示数0或![]() 的点是(N,M)的好点;
的点是(N,M)的好点;
故答案为:0或![]() ;
;
(3)设点P表示的数为n,则
①P为(A,B)的好点时,有:![]() ,
,
解得:![]() ,则
,则![]() 秒;
秒;
②P为(B,A)好点时,有两种情况:
当点P在A、B之间时,有:![]() ,
,
解得:![]() ,则
,则![]() 秒;
秒;
当点P在A点左边时,有:![]() ,
,
解得:![]() ,则
,则![]() 秒;
秒;
③点B是(A、P)的好点时,有:![]() ,
,
解得:![]() ,则
,则![]() 秒;
秒;
④点A是(B,P)的好点时,有:![]() ,
,
解得:![]() ,则
,则![]() 秒;
秒;
⑤点A是(P,B)的好点时,有:![]() ,
,
解得:![]() ,则
,则![]() 秒.
秒.
综合上述,当t为10秒或15秒或20秒或50秒或60秒或80秒时,P、A和B中恰有一个点为其余两点的好点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点对应的数分别-4,8.有一动点P从点A出发第一次向左运动1个单位长度;然后在新的位置第二次运动,向右运动2个单位长度;在此位置第三次运动,向左运动3个单位长度,…按照如此规律不断地左右运动

(1)当运动到第2018次时,求点P所对应的有理数.
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若可能请求出此时点P的位置,若不可能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一列数a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=-2018,a98=-1,且满足任意相邻三个数的和为常数,则a1+a2+a3+…+a98+a99+a100的值为( )
A.1985B.-1985C.2019D.-2019
-
科目: 来源: 题型:
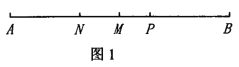
查看答案和解析>>【题目】(1)如图1所示,已知线段AB=20cm,在AB上取一点P,M是AB的中点,N是AP中点,若MN=3cm,求线段AP的长;
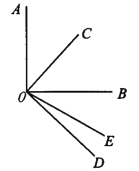
(2)如图2所示,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.则∠COE是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3张纸牌,分別是红桃3、红桃4和黑桃5(简称红3,红4,黑5).把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)两次抽得纸牌均为红桃的概率;(请用“画树状图”或“列表”等方法写出分析过程)
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得花色相同则甲胜,否则乙胜.B方案:若两次抽得纸牌的数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);
(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧
 的长.
的长.
相关试题

