【题目】如图,数轴上A,B两点对应的数分别-4,8.有一动点P从点A出发第一次向左运动1个单位长度;然后在新的位置第二次运动,向右运动2个单位长度;在此位置第三次运动,向左运动3个单位长度,…按照如此规律不断地左右运动
![]()
(1)当运动到第2018次时,求点P所对应的有理数.
(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A的距离的3倍?若可能请求出此时点P的位置,若不可能请说明理由.
参考答案:
【答案】(1)1005;(2)点P运动了第11次和第6次恰好到达这一位置,此时P的位置为-10和-1.
【解析】
(1)往右用加,往左用减,计算即可得出答案;
(2)分三种情况讨论:①当点P在点A左侧时;②当点P在点A和点B之间时;③当点P在点B的右侧时,再分别求出PA和PB所表示的代数式,根据PB=3PA计算,即可得出答案.
解:(1)依题意可得:-4-1+2-3+4-5+…-2017+2018=-4+1009=1005
答:当运动到第2018次时,点P所对应的有理数为1005;
(2)设点P对应的有理数的值为x
①当点P在点A左侧时,PA=-4-x,PB=8-x
依题意可得:8-x=3(-4-x)
解得:x=-10
②当点P在点A和点B之间时,PA=x-(-4)=x+4,PB=8-x
依题意可得:8-x=3(x+4)
解得:x=-1
③当点P在点B的右侧时,PA=x-(-4)=x+4,PB=x-8
依题意可得:x-8=3(x+4)
解得:x=-10,与点P在点B右侧矛盾,故舍去
∴-10和-1分别是点P运动了第11次和第6次到达的位置
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,观察函数y=|x|的图象,写出它的两条的性质;
(2)在图1中,画出函数y=|x-3|的图象;
根据图象判断:函数y=|x-3|的图象可以由y=|x|的图象向 平移 个单位得到;
(3)①函数y=|2x+3|的图象可以由y=|2x|的图象向 平移 单位得到;
②根据从特殊到一般的研究方法,函数y=|kx+3|(k为常数,k≠0)的图象可以由函数y=|kx|(k为常数,k≠0)的图象经过怎样的平移得到.
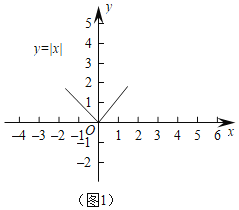
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,B,P,A,C是圆上的点,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =
 ,sin∠PAD =
,sin∠PAD =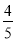 ,则△PAB的面积为_______.
,则△PAB的面积为_______.
-
科目: 来源: 题型:
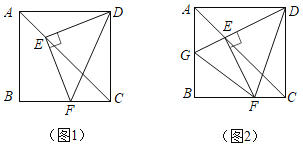
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一列数a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=-2018,a98=-1,且满足任意相邻三个数的和为常数,则a1+a2+a3+…+a98+a99+a100的值为( )
A.1985B.-1985C.2019D.-2019
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解):A,B,C为数轴上三点,若点C到A的距离CA是点C到B的距离CB的2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离CA是2,到点B的距离CB是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离DA是1,到点B的距离DB是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
(知识运用):(1)如图1,表示数______和_______的点是(A,B)的好点;

(2)如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

①表示数______的点是(M,N)的好点;
②表示数______的点是(N,M)的好点;
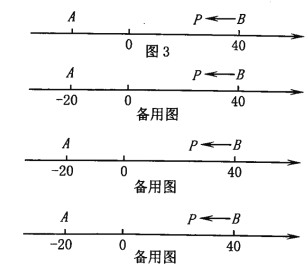
(3)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动.当t为何值时,P、A和B中恰有一个点为其余两点的好点?
相关试题

