【题目】如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交OD于E,连接AD、AE、CE.
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=4,![]() ,求CF的长.
,求CF的长.

参考答案:
【答案】(1)证明见解析,(2)60°;(3)![]()
【解析】
(1)易证∠OEC=∠OCE,∠OEC=∠ECD,从而可知∠OCE=∠ECD,即∠ACE=∠DCE;
(2)延长AE交BC于点G,易证∠AGC=∠B+∠BAG=60°,由于OE∥BC,所以∠AEO=∠AGC=60°,所以∠EAO=∠AEO=60°;
(3)易证![]() ,由于
,由于![]() ,所以
,所以![]() =
=![]() ,由圆周角定理可知∠AEC=∠FDC=90°,从而可证明△CDF∽△CEA,利用三角形相似的性质即可求出答案.
,由圆周角定理可知∠AEC=∠FDC=90°,从而可证明△CDF∽△CEA,利用三角形相似的性质即可求出答案.
(1)∵OC=OE,∴∠OEC=∠OCE.
∵OE∥BC,∴∠OEC=∠ECD,∴∠OCE=∠ECD,即∠ACE=∠DCE;
(2)延长AE交BC于点G.
∵∠AGC是△ABG的外角,∴∠AGC=∠B+∠BAG=60°.
∵OE∥BC,∴∠AEO=∠AGC=60°.
∵OA=OE,∴∠EAO=∠AEO=60°.
(3)∵O是AC中点,∴![]()
![]() ,∴
,∴![]() =
=![]() .
.
∵AC是直径,∴∠AEC=∠FDC=90°.
∵∠ACE=∠FCD,∴△CDF∽△CEA,∴![]() =
=![]() ,∴CF=
,∴CF=![]() CA=
CA=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
,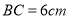 ,
, 交
交 于点
于点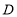 .动点
.动点 从点
从点 出发,按
出发,按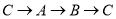 的路径运动,且速度为
的路径运动,且速度为 ,设出发时间为
,设出发时间为 .
.
(1)求
 的长.
的长.(2)当
 时,求证:
时,求证: .
.(3)当点
 在
在 边上运动时,若
边上运动时,若 是以
是以 为腰的等腰三角形,求出所有满足条件的
为腰的等腰三角形,求出所有满足条件的 的值.
的值.(4)在整个运动过程中,若
 (
( 为正整数),则满足条件的
为正整数),则满足条件的 的值有________个.
的值有________个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=kx+b 经过点A(﹣
 ,0)和点B(2,5).
,0)和点B(2,5).(1)求直线l1与y轴的交点坐标;
(2)若点C(a,a+2)与点D在直线l1上,过点D的直线l2与x轴正半轴交于点 E,当AC=CD=CE 时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y1=ax2﹣
 x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0, ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

相关试题

