【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.

(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)应用待定系数法求解析式;
(2)设出点T坐标,表示△TAC三边,进行分类讨论;
(3)设出点P坐标,表示Q、R坐标及PQ、QR,根据以P,Q,R为顶点的三角形与△AMG全等,分类讨论对应边相等的可能性即可.
(1)由已知,c=![]() ,
,
将B(1,0)代入,得:a﹣![]() =0,
=0,
解得a=﹣![]() ,
,
抛物线解析式为y1=![]() x2-
x2-![]() x+
x+![]() ,
,
∵抛物线y1平移后得到y2,且顶点为B(1,0),
∴y2=﹣![]() (x﹣1)2,
(x﹣1)2,
即y2=-![]() x2+
x2+![]() x-
x-![]() ;
;
(2)存在,
如图1:
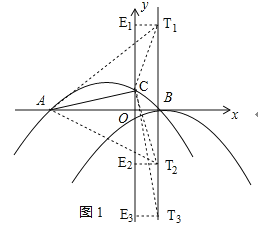
抛物线y2的对称轴l为x=1,设T(1,t),
已知A(﹣3,0),C(0,![]() ),
),
过点T作TE⊥y轴于E,则
TC2=TE2+CE2=12+(![]() )2=t2﹣
)2=t2﹣![]() t+
t+![]() ,
,
TA2=TB2+AB2=(1+3)2+t2=t2+16,
AC2=![]() ,
,
当TC=AC时,t2﹣![]() t+
t+![]() =
=![]() ,
,
解得:t1=![]() ,t2=
,t2=![]() ;
;
当TA=AC时,t2+16=![]() ,无解;
,无解;
当TA=TC时,t2﹣![]() t+
t+![]() =t2+16,
=t2+16,
解得t3=﹣![]() ;
;
当点T坐标分别为(1,![]() ),(1,
),(1,![]() ),(1,﹣
),(1,﹣![]() )时,△TAC为等腰三角形;
)时,△TAC为等腰三角形;
(3)如图2:
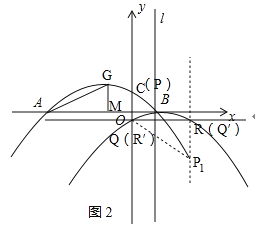
设P(m,![]() ),则Q(m,
),则Q(m,![]() ),
),
∵Q、R关于x=1对称
∴R(2﹣m,![]() ),
),
①当点P在直线l左侧时,
PQ=1﹣m,QR=2﹣2m,
∵△PQR与△AMG全等,
∴当PQ=GM且QR=AM时,m=0,
∴P(0,![]() ),即点P、C重合,
),即点P、C重合,
∴R(2,﹣![]() ),
),
由此求直线PR解析式为y=﹣![]() x+
x+![]() ,
,
当PQ=AM且QR=GM时,无解;
②当点P在直线l右侧时,
同理:PQ=m﹣1,QR=2m﹣2,
则P(2,﹣![]() ),R(0,﹣
),R(0,﹣![]() ),
),
PQ解析式为:y=﹣![]() ;
;
∴PR解析式为:y=﹣![]() x+
x+![]() 或y=﹣
或y=﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=kx+b 经过点A(﹣
 ,0)和点B(2,5).
,0)和点B(2,5).(1)求直线l1与y轴的交点坐标;
(2)若点C(a,a+2)与点D在直线l1上,过点D的直线l2与x轴正半轴交于点 E,当AC=CD=CE 时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交OD于E,连接AD、AE、CE.
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=4,
 ,求CF的长.
,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x﹣4上,则⊙A的半径为( )
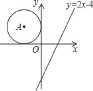
A.
 B. 2 C. 4 D. 6
B. 2 C. 4 D. 6
相关试题

