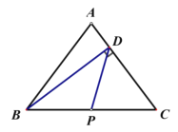
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .动点
.动点![]() 从点
从点![]() 出发,按
出发,按![]() 的路径运动,且速度为
的路径运动,且速度为![]() ,设出发时间为
,设出发时间为![]() .
.

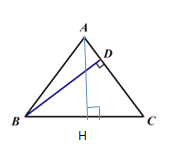
(1)求![]() 的长.
的长.
(2)当![]() 时,求证:
时,求证:![]() .
.
(3)当点![]() 在
在![]() 边上运动时,若
边上运动时,若![]() 是以
是以![]() 为腰的等腰三角形,求出所有满足条件的
为腰的等腰三角形,求出所有满足条件的![]() 的值.
的值.
(4)在整个运动过程中,若![]() (
(![]() 为正整数),则满足条件的
为正整数),则满足条件的![]() 的值有________个.
的值有________个.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)见解析;(4) 无数个.
;(2)见解析;(3)见解析;(4) 无数个.
【解析】
(1)利用等腰三角形的性质和勾股定理求三角形的高AH的长度,然后根据三角形的面积法求BD的长;(2)根据题意计算出AP=AD,然后利用SAS定理证明![]() ,从而利用全等三角形的性质进行证明;(3)分情况讨论当CP=CD或CP=DP时,分别求此时CP的长度,从而求t的值;(4)根据题意求出
,从而利用全等三角形的性质进行证明;(3)分情况讨论当CP=CD或CP=DP时,分别求此时CP的长度,从而求t的值;(4)根据题意求出![]() ,从而确定三角形面积的值有无数个,所以t的值有无数个.
,从而确定三角形面积的值有无数个,所以t的值有无数个.
(1)解:过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
(2)当![]() 时,
时,![]()
此时点![]() 在
在![]() 边上,且
边上,且![]()
由(1)可得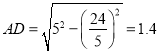
∴![]()
∵![]() .
. ![]()
∴![]()
∴![]()
∴![]()
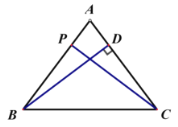
(3)当点img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/10/c88d1317/SYS202011271015219315411118_DA/SYS202011271015219315411118_DA.016.png" width="15" height="16" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />在![]() 边上运动时,
边上运动时,![]()
①当![]() 时,
时,![]() 是等腰三角形
是等腰三角形
∵![]()
∴![]()
∴![]()
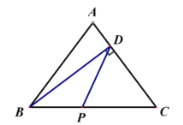
②当![]() 时,
时,![]() 是等腰三角形
是等腰三角形
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() 为
为![]() 中点
中点
∴![]()
∴![]()
∴![]()
∴当![]() 是以
是以![]() 为腰的等腰三角形时,
为腰的等腰三角形时,![]() 的值为6.2或6.5.
的值为6.2或6.5.
(4)由(1)得知![]()
![]()
∴![]()
又∵n为正整数,
∴![]() 的值有无数个
的值有无数个
∴满足条件的![]() 的值无数个.
的值无数个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=
 (x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.
(x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.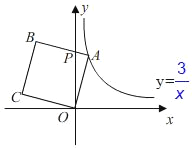
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处.
(1)如图1,若折痕
 ,且
,且 ,求矩形ABCD的周长;
,求矩形ABCD的周长;(2)如图2,在AD边上截取DG=CF,连接GE,BD,相交于点H,求证:BD⊥GE.
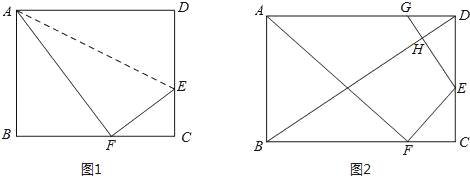
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=kx+b 经过点A(﹣
 ,0)和点B(2,5).
,0)和点B(2,5).(1)求直线l1与y轴的交点坐标;
(2)若点C(a,a+2)与点D在直线l1上,过点D的直线l2与x轴正半轴交于点 E,当AC=CD=CE 时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交OD于E,连接AD、AE、CE.
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=4,
 ,求CF的长.
,求CF的长.
相关试题

