【题目】如图,台风中心位于点![]() ,并沿东北方向
,并沿东北方向![]() 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,![]() 市位于点
市位于点![]() 的北偏东75°方向上,距离
的北偏东75°方向上,距离![]() 点480千米.
点480千米.

(1)说明本次台风是否会影响![]() 市;
市;
(2)若这次台风会影响![]() 市,求
市,求![]() 市受台风影响的时间.
市受台风影响的时间.
参考答案:
【答案】(1)本次台风会影响B市.(2)B市受台风影响的时间为5小时.
【解析】
(1)作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与260千米相比较即可.
(2)以B为圆心,以260为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.
(1)作BH⊥PQ于点H.
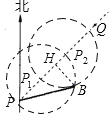
在Rt△BHP中,
由条件知,PB=480,∠BPQ=75°-45°=30°,
∴BH=480sin30°=240<260,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.
由(1)得BH=240,由条件得BP1=BP2=260,
∴P1P2=![]() =200,
=200,
∴台风影响的时间t=![]() =5(小时).
=5(小时).
故B市受台风影响的时间为5小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E在BC上,AB=BE,BF平分∠ABC交AD于点F,请用无刻度的直尺画图(保留作图痕迹,不写画法).
(1)在图1中,过点A画出△ABF中BF边上的高AG;
(2)在图2中,过点C画出C到BF的垂线段CH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.

(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,等腰
 和等腰
和等腰 中,
中, ,
, ,
, ,
, 三点在同一直线上,求证:
三点在同一直线上,求证: ;
;(2)如图2,等腰
 中,
中, ,
, ,
, 是三角形外一点,且
是三角形外一点,且 ,求证:
,求证: ;
;(3)如图3,等边
 中,
中, 是形外一点,且
是形外一点,且 ,
, ①
 的度数为 ;
的度数为 ;②
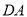 ,
,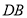 ,
, 之间的关系是 .
之间的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为
 (即tan∠PAB=
(即tan∠PAB=  ),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
相关试题

