【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为 ![]() (即tan∠PAB=
(即tan∠PAB= ![]() ),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
参考答案:
【答案】解:①作PE⊥OB于点E,PF⊥CO于点F,

在Rt△AOC中,AO=200米,∠CAO=60°,
∴CO=AOtan60°=200 ![]() (米)
(米)
②设PE=x米,
∵tan∠PAB= ![]() =
= ![]() ,
,
∴AE=3x.
在Rt△PCF中,
∠CPF=45°,CF=200 ![]() ﹣x,PF=OA+AE=200+3x,
﹣x,PF=OA+AE=200+3x,
∵PF=CF,
∴200+3x=200 ![]() ﹣x,
﹣x,
解得x=50( ![]() ﹣1)米.
﹣1)米.
答:电视塔OC的高度是200 ![]() 米,所在位置点P的铅直高度是50(
米,所在位置点P的铅直高度是50( ![]() ﹣1)米.
﹣1)米.
【解析】①作PE⊥OB于点E,PF⊥CO于点F,在Rt△AOC中利用正切定义得CO=AOtan60°即可;②设PE=x米利用坡度定义得∵tan∠PAB= ![]() AE=3x.利用等腰三角形的性质得200+3x=200
AE=3x.利用等腰三角形的性质得200+3x=200 ![]() ﹣x,即可。
﹣x,即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,台风中心位于点
 ,并沿东北方向
,并沿东北方向 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米, 市位于点
市位于点 的北偏东75°方向上,距离
的北偏东75°方向上,距离 点480千米.
点480千米.
(1)说明本次台风是否会影响
 市;
市;(2)若这次台风会影响
 市,求
市,求 市受台风影响的时间.
市受台风影响的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.

(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,等腰
 和等腰
和等腰 中,
中, ,
, ,
, ,
, 三点在同一直线上,求证:
三点在同一直线上,求证: ;
;(2)如图2,等腰
 中,
中, ,
, ,
, 是三角形外一点,且
是三角形外一点,且 ,求证:
,求证: ;
;(3)如图3,等边
 中,
中, 是形外一点,且
是形外一点,且 ,
, ①
 的度数为 ;
的度数为 ;②
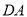 ,
,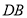 ,
, 之间的关系是 .
之间的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某人到一家快递公司办理环江香米(简称香米)的快递托运,重量为
 千克.快递公司收取托运费方案如下:
千克.快递公司收取托运费方案如下:凡物品重量不超过10千克的,按2元/千克收取托运费;当物品重量超过10千克的,超出部分按3元/千克加收托运费.
(1)写出
 千克香米的托运费的表达式 (用含字母
千克香米的托运费的表达式 (用含字母 的式子表示);
的式子表示);(2)若托运香米重量为
 千克时,求出这笔托运费.
千克时,求出这笔托运费. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

相关试题

