【题目】如图，在△ABC中，AC=BC=6,∠ACB＞90°,∠ABC的平分线交AC于点D，E是AB上一点，且BE=BC，CF∥ED交BD于点F，连接EF,ED.

（1）求证：四边形CDEF是菱形．

（2）当∠ACB＝ 度时，四边形CDEF是正方形，请给予证明；并求此时正方形的边长。

参考答案：

【答案】（1）详见解析；（2）当∠ACB＝120度时，四边形CDEF是正方形，证明见解析，此时正方形的边长为 .

【解析】

（1）先证△CBD≌△EBD，由全等三角形的性质得DE=DC，∠BDC=∠BDE，同理△BCF≌△BEF，EF=CF，再根据平行线的性质得∠CFD=∠BDE，等量代换得CFD=∠BDC，可得CF=CD，根据四边相等的四边形是菱形可得结论；

（2）当∠ACB＝120度时，四边形CDEF是正方形.由等腰三角形的性质可得∠A=∠ABC=30°，由角平分线得∠CBD=∠EBD=15°，根据平行线的性质得∠BEF=∠A=30°，再由三角形外角的性质可得∠EFD=∠EBD+∠BEF=45°，由菱形的性质可证出∠EFD=∠EDF=45°，则∠FED=90°，菱形CDEF是正方形；设正方形CDEF的边长为x，在Rt△ADE中，利用30°角的直角三角形的性质表示出AD=x，由AB=AC=6可得AD=6-x,则6-x =x，解方程即可求得正方形的边长.

（1）证明：∵BD平分∠ABC

∴∠CBD=∠EBD，

在△CBD和△EBD中

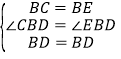∴△CBD≌△EBD（SAS）

∴DE=DC，∠BDC=∠BDE

同理△BCF≌△BEF

∴EF=CF

∵CF∥ED ∴∠CFD=∠BDE

∴∠CFD=∠BDC

∴CF=CD

∴EF=CF=CD=DE

∴四边形CDEF是菱形

（2）当∠ACB＝ 120 度时，四边形CDEF是正方形

证明：∵AC=BC ∠ACB＝ 120°

∴∠A=∠ABC=30°

∵BD平分∠ABC

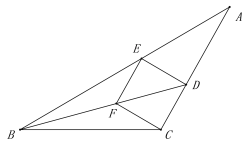
∴∠CBD=∠EBD=15°

∵四边形CDEF是菱形

∴EF∥AC

∴∠BEF=∠A=30°

∴∠EFD=∠EBD+∠BEF=15°+30°=45°,

∵EF=ED

∴∠EFD=∠EDF=45°

∴∠FED=90°

∴菱形CDEF是正方形.

设正方形CDEF的边长为x，

在Rt△ADE中，∠A=30° ∴AE=2x, AD=,

∵AD+CD=AC=6

∴+x=6 ∴x=

∴正方形CDEF的边长为.

故答案为：（1）详见解析；（2）当∠ACB＝120度时，四边形CDEF是正方形，证明见解析，此时正方形的边长为 .

关闭