【题目】如图,在□ABCD中,点E在BC上,AB=BE,BF平分∠ABC交AD于点F,请用无刻度的直尺画图(保留作图痕迹,不写画法).
(1)在图1中,过点A画出△ABF中BF边上的高AG;
(2)在图2中,过点C画出C到BF的垂线段CH.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接AE,交BF于点G,则AG即为所求,理由为:AB=AE,BF平分∠ABC,根据等腰三角形三线合一的性质可得BG⊥AG;
(2)连接AC、BD交于点O,连接EO并延长交AD于点G,连接CG交BF于点H,CH即为所求,理由:由平行四边形的性质以及作法可得△BOE≌△DOG,由此可得DG=BE=AB=CD,继而可得CG平分∠BCD,由AB//CD可得∠ABC+∠BCD=180°,继而可得∠FBC+∠GCB=90°,即∠BHC=90°,由此即可得答案.
(1)如图1,AG即为所求;
(2)如图2,CH即为所求.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,台风中心位于点
 ,并沿东北方向
,并沿东北方向 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米, 市位于点
市位于点 的北偏东75°方向上,距离
的北偏东75°方向上,距离 点480千米.
点480千米.
(1)说明本次台风是否会影响
 市;
市;(2)若这次台风会影响
 市,求
市,求 市受台风影响的时间.
市受台风影响的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.

(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,等腰
 和等腰
和等腰 中,
中, ,
, ,
, ,
, 三点在同一直线上,求证:
三点在同一直线上,求证: ;
;(2)如图2,等腰
 中,
中, ,
, ,
, 是三角形外一点,且
是三角形外一点,且 ,求证:
,求证: ;
;(3)如图3,等边
 中,
中, 是形外一点,且
是形外一点,且 ,
, ①
 的度数为 ;
的度数为 ;②
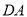 ,
,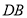 ,
, 之间的关系是 .
之间的关系是 .
相关试题

