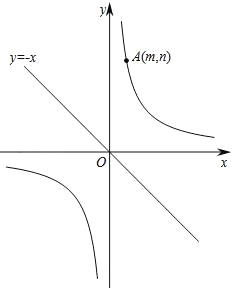
【题目】如图,已知直线y=﹣x和双曲线![]() (k>0),点A(m,n)(m>0)在双曲线
(k>0),点A(m,n)(m>0)在双曲线![]() 上.
上.
(1)当m=n=2时,
①直接写出k的值;
②将直线y=﹣x作怎样的平移能使平移后的直线与双曲线![]() 只有一个交点.
只有一个交点.
(2)将直线y=﹣x绕着原点O旋转,设旋转后的直线与双曲线![]() 交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:
交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:![]() 与
与![]() 的值存在怎样的数量关系?请说明理由.
的值存在怎样的数量关系?请说明理由.
参考答案:
【答案】(1)①k=4;②只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点;(2)综上所述,![]() .理由见试题解析.
.理由见试题解析.
【解析】
试题分析:(1)①当m=n=2时,得出A(2,2),把点A(2,2)代入双曲线![]() (k>0)求出k的值即可;
(k>0)求出k的值即可;
②设平移后的直线解析式为y=﹣x+b1,由直线和双曲线解析式组成方程组,整理可得方程:x2﹣b1x+4=0,当判别式=0时,求出b1=±4即可;
(2)分两种情况讨论:由双曲线的对称性可知,C(﹣a,﹣b),①当点A在直线BC的上方时,过A、B、C分别作y轴的垂线,垂足分别为F、G、H,则OF=n,OG=OH=b,得出FG=OF﹣OG=n﹣b,FH=OF+OH=n+b,由平行线得出比例式,即可得出结论;
②当点A在直线BC的下方时,同理可得出结论;即可得出结果.
试题解析:(1)①当m=n=2时,A(2,2),
把点A(2,2)代入双曲线![]() (k>0)得:k=2×2=4;
(k>0)得:k=2×2=4;
②设平移后的直线解析式为y=﹣x+b1,由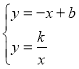 可得,
可得,![]() ,
,
整理可得:x2﹣b1x+4=0,当△=![]() -4×1×4=0,即b1=±4时,方程x2﹣b1x+4=0有两个相等的实数根,此时直线y=﹣x+b1与双曲线只有一个交点,∴只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点;
-4×1×4=0,即b1=±4时,方程x2﹣b1x+4=0有两个相等的实数根,此时直线y=﹣x+b1与双曲线只有一个交点,∴只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点;
(2)![]() =2,理由如下:
=2,理由如下:
分两种情况讨论:由双曲线的对称性可知,C(﹣a,﹣b)
①当点A在直线BC的上方时,如图所示:过A、B、C分别作y轴的垂线,垂足分别为F、G、H,
则OF=n,OG=OH=b,∴FG=OF﹣OG=n﹣b,FH=OF+OH=n+b,
∵AF∥BG∥x轴,∴![]() ,∵AF∥x轴∥CH,
,∵AF∥x轴∥CH,
∴![]() ,∴
,∴![]() =2;
=2;
②当点A在直线BC的下方时,
同理可求:![]() ,
, ![]() ,
,
∴![]() ;
;
综上所述,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:8a6÷2a2+4a32a﹣(3a2)2
-
科目: 来源: 题型:
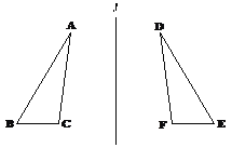
查看答案和解析>>【题目】如图所示,是用笔尖扎重叠的纸得到的成轴对称的图案,请根据图形写出:
(1)两组对应点:__________和__________;
(2)两组对应线段:__________和__________;
(3)两组对应角:__________和__________.
-
科目: 来源: 题型:
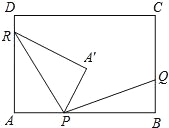
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.
(1)若k=4,PA=15,则四边形PARA′的形状是 ;
(2)设DR=x,点B关于直线PQ的对称点为B′点.
①记△PRA′的面积为S1,△PQB′的面积为S2.当S1<S2时,求相应x的取值范围及S2﹣S1的最大值;(用含k的代数式表示)
②在点P的运动过程中,判断点B′能否与点A′重合?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将抛物线y=x2﹣4先向右平移两个单位,再向上平移两个单位,得到的抛物线的解析式是( )
A.y=(x+2)2+2
B.y=(x﹣2)2﹣2
C.y=(x﹣2)2+2
D.y=(x+2)2﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】27的立方根为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(2,y1)、B(3,y2)是二次函数y=x2﹣2x+1的图象上两点,则y1与y2的大小关系为y1y2(填“>”、“<”、“=”).
相关试题

