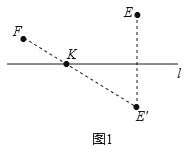
【题目】如图1,点EF在直线l的同一侧,要在直线l上找一点K,使KE与KF的距离之和最小,我们可以作出点E关于l的对称点E′,连接FE′交直线L于点K,则点K即为所求.
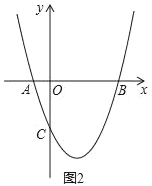
(1)(实践运用)抛物线y=ax2+bx+c经过点A(﹣1,0)、B(3,0)、C(0,﹣3).如图2.
①求该抛物线的解析式;
②在抛物线的对称轴上找一点P,使PA+PC的值最小,并求出此时点P的坐标及PA+PC的最小值.
(2)(知识拓展)在对称轴上找一点Q,使|QA﹣QC|的值最大,并求出此时点Q的坐标.
参考答案:
【答案】(1)①y=x2﹣2x﹣3,②点P的坐标为(1,﹣2),PA+PC的最小值为3![]() ;(2)点Q的坐标为(1,﹣6).
;(2)点Q的坐标为(1,﹣6).
【解析】分析:(1)①由点A、B的坐标可将抛物线的解析式变形为交点式,代入点C的坐标即可求出a值,此题得解;
②由点A、B关于抛物线的对称轴对称可得出连接BC交抛物线对称轴于点P,此时PA+PC的值最小,根据抛物线的解析式可求出其对称轴为直线x=1,由点B、C的坐标利用待定系数法可求出过点B、C的直线的解析式,代入x=1求出y值,由此即可得出点P的坐标,再利用勾股定理求出线段BC的长即可;
(2)连接AC并延长AC交抛物线对称轴与点Q,此时|QA﹣QC|的值最大,且|QA﹣QC|的最大值为线段AC的长(三角形两边之差小于第三边),由点A、C的坐标利用待定系数法可求出过点A、C的直线的解析式,代入x=1求出y值,由此即可得出点Q的坐标,此题得解.
详解:(1)①∵抛物线与x轴的交点为A(﹣1,0)、B(3,0),∴抛物线的解析式为y=a(x+1)(x﹣3).
∵抛物线过点C(0,﹣3),∴﹣3=(0+1)×(0﹣3)a,∴a=1,∴该抛物线的解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3.
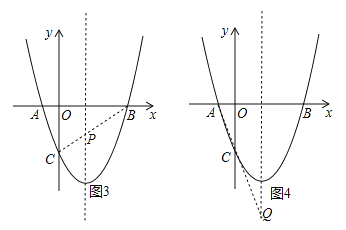
②∵点A、B关于抛物线的对称轴对称,∴连接BC交抛物线对称轴于点P,此时PA+PC的值最小,如图3所示.
∵抛物线的解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴为直线x=1.
利用待定系数法可求出过点B、C的直线为y=x﹣3,当x=1时,y=x﹣3=1﹣3=﹣2,∴点P的坐标为(1,﹣2),PA+PC的最小值为BC=![]() =3
=3![]() .
.
(2)连接AC并延长AC交抛物线对称轴与点Q,此时|QA﹣QC|的值最大,且|QA﹣QC|的最大值为线段AC的长,如图4所示.
利用待定系数法可求出过点A、C的直线为y=﹣3x﹣3,当x=1时,y=﹣3x﹣3=﹣3×1﹣3=﹣6,∴点Q的坐标为(1,﹣6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题一:如图1,已知A,C两点之间的距离为16 cm,甲,乙两点分别从相距3cm的A,B两点同时出发到C点,若甲的速度为8 cm/s,乙的速度为6 cm/s,设乙运动时间为x(s), 甲乙两点之间距离为y(cm).
(1)当甲追上乙时,x = .
(2)请用含x的代数式表示y.
当甲追上乙前,y= ;
当甲追上乙后,甲到达C之前,y= ;
当甲到达C之后,乙到达C之前,y= .

问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 cm;时针OE指向圆周上的点的速度为每分钟转动 cm.
(2)若从4:00起计时,求几分钟后分针与时针第一次重合.

-
科目: 来源: 题型:
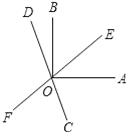
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简再求值:
 ,其中a、b满足
,其中a、b满足
(2)已知a+b=4,ab=-2,求代数式(5a-4b-4ab)-3(a-2b-ab)的值.
-
科目: 来源: 题型:
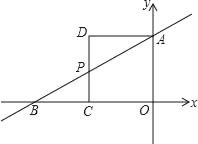
查看答案和解析>>【题目】如图,在直角坐标系中,直线AB分别与x轴、y轴交于B、A两点,OA、OB的长是关于x的一元二次方程x2﹣12x+32=0的两个实数根,且OB>OA,以OA为一边作如图所示的正方形AOCD,CD交AB于点P.
(1)求直线AB的解析式;
(2)在x轴上是否存在一点Q,使以P、C、Q为顶点的三角形与△ADP相似?若存在,求点Q坐标;否则,说明理由;
(3)设N是平面内一动点,在y轴上是否存在点M,使得以A、C、M、N为顶点的四边形是菱形?若存在,请直接写出点M的坐标;否则,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,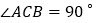 ,将
,将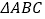 绕顶点
绕顶点 逆时针旋转得到Rt△DEC,点M是BC的中点,点P是DE的中点,连接PM,若BC =2,∠BAC=30°,则线段PM的最大值是 ( )
逆时针旋转得到Rt△DEC,点M是BC的中点,点P是DE的中点,连接PM,若BC =2,∠BAC=30°,则线段PM的最大值是 ( )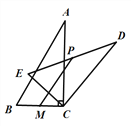
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
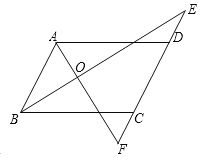
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:
①∠BAD=2∠F;②∠E+∠F=90°.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)AD∥BC,理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠______, (____________________________)
∴ AD∥BC (____________________________)
(2)AB与EF的位置关系是:_______________.
∵BE平分∠ABC, (已知)
∴∠ABE=
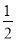 ∠ABC. (角平分线的定义)
∠ABC. (角平分线的定义)又∵∠ABC=2∠E, (已知),
即∠E=
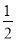 ∠ABC,
∠ABC,∴∠E=∠_____. (_____________________________)
∴ ______∥_____. (_____________________________)
相关试题

