【题目】如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
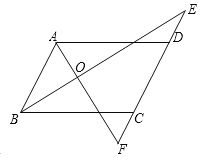
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:
①∠BAD=2∠F;②∠E+∠F=90°.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)AD∥BC,理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠______, (____________________________)
∴ AD∥BC (____________________________)
(2)AB与EF的位置关系是:_______________.
∵BE平分∠ABC, (已知)
∴∠ABE=![]() ∠ABC. (角平分线的定义)
∠ABC. (角平分线的定义)
又∵∠ABC=2∠E, (已知),
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠_____. (_____________________________)
∴ ______∥_____. (_____________________________)
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)①详见解析.②详见解析.
【解析】
(1)根据平行线的判定,以及证明题的书写规则解题即可
(2)根据平行线的判定以及书写规则解题即可
(3)①结合(1)中结论以及角平分线可证得∠BAD=2∠F.;
②根据(1)中结论,利用平行线的性质,以及角的等量代换即可求解
解:(1)AD∥BC,理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠ BCF ,(同角的补角相等_______ )
∴ AD∥BC;(同位角相等,两直线平行 );
(2)AB与EF的位置关系是: AB∥EF _.
∵BE平分∠ABC(已知)
∴∠ABE=![]() ∠ABC(角平分线的定义)
∠ABC(角平分线的定义)
又∵∠ABC=2∠E, (已知) ,
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠_ABE .(_等量代换_)
∴ __AB ∥_EF (内错角相等,两直线平行 );
(3)①由( 1)知AB∥EF,
∴∠BAF=∠F.
∵AF平分∠BAD,
∴∠BAD=2∠BAF,
∴∠BAD=2∠F.
②由( 1)知AD∥BC,
∴∠BAD+∠ABC=180°,
∵∠BAD=2∠F,∠ABC=2∠E,
∴∠E+∠F=90°.
-
科目: 来源: 题型:
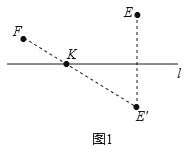
查看答案和解析>>【题目】如图1,点EF在直线l的同一侧,要在直线l上找一点K,使KE与KF的距离之和最小,我们可以作出点E关于l的对称点E′,连接FE′交直线L于点K,则点K即为所求.
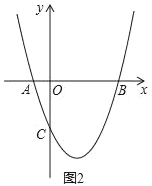
(1)(实践运用)抛物线y=ax2+bx+c经过点A(﹣1,0)、B(3,0)、C(0,﹣3).如图2.
①求该抛物线的解析式;
②在抛物线的对称轴上找一点P,使PA+PC的值最小,并求出此时点P的坐标及PA+PC的最小值.
(2)(知识拓展)在对称轴上找一点Q,使|QA﹣QC|的值最大,并求出此时点Q的坐标.
-
科目: 来源: 题型:
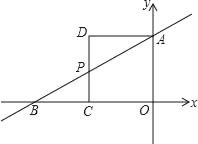
查看答案和解析>>【题目】如图,在直角坐标系中,直线AB分别与x轴、y轴交于B、A两点,OA、OB的长是关于x的一元二次方程x2﹣12x+32=0的两个实数根,且OB>OA,以OA为一边作如图所示的正方形AOCD,CD交AB于点P.
(1)求直线AB的解析式;
(2)在x轴上是否存在一点Q,使以P、C、Q为顶点的三角形与△ADP相似?若存在,求点Q坐标;否则,说明理由;
(3)设N是平面内一动点,在y轴上是否存在点M,使得以A、C、M、N为顶点的四边形是菱形?若存在,请直接写出点M的坐标;否则,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
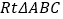 中,
中,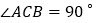 ,将
,将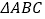 绕顶点
绕顶点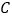 逆时针旋转得到Rt△DEC,点M是BC的中点,点P是DE的中点,连接PM,若BC =2,∠BAC=30°,则线段PM的最大值是 ( )
逆时针旋转得到Rt△DEC,点M是BC的中点,点P是DE的中点,连接PM,若BC =2,∠BAC=30°,则线段PM的最大值是 ( )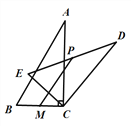
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
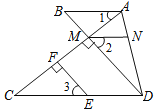
查看答案和解析>>【题目】如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A、B两种计算器共100个,要求A种计算器数量不低于B种的
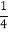 ,且不高于B种的
,且不高于B种的 .已知买1个A种计算器和1个B种计算器共需250元,买2个A种计算器和3个B种计算器的费用相等。
.已知买1个A种计算器和1个B种计算器共需250元,买2个A种计算器和3个B种计算器的费用相等。(1)求两种计算器的单价。
(2)求如何购买可使总费用最低。
(3)由于市场行情波动,实际购买时,A种计算器单价下调m元(m>0),同时B种计算器单价上调了m元,此时购买这两种计算器所需最少费用为12200元,求m的值。
-
科目: 来源: 题型:
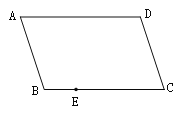
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
相关试题

