Question

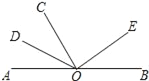
【题目】已知，射线BC∥射线OA，∠C=∠BAO=100°，试回答下列问题：

（1）如图①，求证：OC∥AB；

（2）若点E、F在线段BC上，且满足∠EOB=∠AOB，并且OF平分∠BOC，

①如图②，若∠AOB=30°，则∠EOF的度数等于多少（直接写出答案即可）；

②若平行移动AB，当∠BOC=6∠EOF时，求∠ABO．

Answer 1

【答案】（1）证明见解析；（2）Ⅰ）∠EOF=5°；Ⅱ）∠ABO=48°．

【解析】

（1）只要证明∠COA+∠OAB=180°即可；
（2）Ⅰ）如图②，根据∠EOF=∠COF-∠COE，只要求出∠COF，∠COE即可；
Ⅱ）设∠EOF=x，则∠BOC=6x，∠BOF=3x，∠BOE=∠AOB=4x，构建方程即可解决问题；

（1）∵BC∥OA，

∴∠C+∠COA=180°，∠BAO+∠ABC=180°，

∵∠C=∠BAO=100°，

∴∠COA=∠ABC=80°，

∴∠COA+∠OAB=180°，

∴OC∥AB．

（2）Ⅰ）∵∠AOB=∠EOB=30°，∠AOC=50°，

∴∠COE=80°﹣60°=20°，∠COB=80°﹣30°=50°，

∵CF平分∠COB，

∴∠COF=∠COB=25°，

∴∠EOF=25°﹣20°=5°，

Ⅱ）设∠EOF=x，则∠BOC=6x，∠BOF=3x，∠BOE=∠AOB=4x，

∵∠AOB+∠BOC+∠OCB=180°，

∴4x+6x+100°=180°，

∴x=8°，

∴∠ABO=∠BOC=6x=48°．