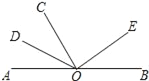
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
(1)图中有多少个小于180°的角?
(2)若OE平分∠BOC,求∠DOE的度数;
(3)若∠COE=2∠BOE,∠DOE=108°,求∠COE的度数.
参考答案:
【答案】(1)图中有9个小于180°的角;(2)∠DOE=90°;(3)∠COE═72°.
【解析】
(1)根据角的定义,按照一定的规律计数即可;
(2)依据角平分线的定义可知∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,然后逆用乘法的分配律可求得∠DOE=90°;
∠BOC,然后逆用乘法的分配律可求得∠DOE=90°;
(3)设∠BOE=x,然后依据∠DOE=108°列方程求解即可.
(1)图中小于180°的角有∠AOD、∠AOC、∠AOE、∠DOC、∠DOE、∠DOB、∠COE、∠COB、∠EOB共9个;
(2)∵OD平分∠AOC,OE平分∠BOC,
∴![]() ,
,![]() .
.
∵∠AOC+∠BOC=180°,
∴![]() .
.
∴∠DOE=∠COD+∠COE=90°.
(3)设∠BOE=x,
∵∠COE=2∠BOE,∴∠COE=2x,
∴∠AOC=180°﹣3x.
∵OD平分∠AOC,
∴![]() .
.
∵∠COD+∠COE═∠DOE=108°,
∴![]() ,x=36°.
,x=36°.
∴∠COE═72°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:

(1)AF=CG;
(2)CF=2DE. -
科目: 来源: 题型:
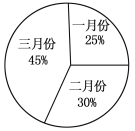
查看答案和解析>>【题目】某服装专卖店老板对第一季度男、女服装销售收入进行统计,并绘制了扇形统计图.如图,由于三月份开展促销活动,男、女服装的销售收入分别比二月份增长了40%,64%,已知第一季度男女服装销售总收入为20万元.
(1)一月份销售收入为____万元,二月份销售收入为____万元,三月份的销售收入为____万元;
(2)二月份男、女服装的销售收入分别是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
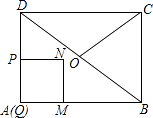
(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10﹣14吨/月范围,并将调查结果制成了如图所示的条形统计图.

(1)请将条形统计图补充完整;
(2)这50户家庭月用水量的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,射线BC∥射线OA,∠C=∠BAO=100°,试回答下列问题:
(1)如图①,求证:OC∥AB;
(2)若点E、F在线段BC上,且满足∠EOB=∠AOB,并且OF平分∠BOC,
①如图②,若∠AOB=30°,则∠EOF的度数等于多少(直接写出答案即可);
②若平行移动AB,当∠BOC=6∠EOF时,求∠ABO.

相关试题

