【题目】如图,在等腰△ABC中,BA=BC,∠ABC=100°,AB平分∠WAC.在线段AC上有一动点D,连接BD并作∠DBE,使∠DBE=50°,BE边交直线AW于点E,连接DE.
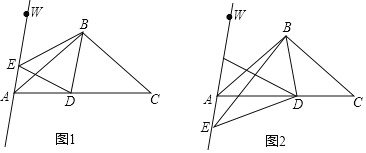
(1)如图1,当点E在射线AW上时,直接判断:AE+DE CD;(填“>”、“=”或“<”)
(2)如图2,当点E在射线AW的反向延长线上时,
①判断线段CD,DE,AE之间的数量关系,并证明;
②若S四边形ABDE﹣S△BCD=6,且2DE=5AE,AD=![]() AE,求S△ABC的值.
AE,求S△ABC的值.
参考答案:
【答案】(1)=;(2)①DE=CD+AE.理由见解析;②S△ABC=![]() .
.
【解析】
(1)在AC上取一点T,使得∠TBD=![]() ∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
(2)①在AC的延长线上取一点T,使得∠TBD=![]() ∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
②根据全等三角形的性质可得:S△ABE=S△BCT,S△BDE=S△BDT,然后根据已知条件可得S△BCT=3,设DE=5k,AE=2k,然后利用k求出AC:CT,最后根据同高时,三角形的面积之比等于底之比即可求出S△ABC的值.
解:(1)如图1中,在AC上取一点T,使得∠TBD=![]() ∠ABC,连接BT.
∠ABC,连接BT.
∵∠TBD=![]() ∠ABC,∠DBE=50°=
∠ABC,∠DBE=50°=![]() ∠ABC,
∠ABC,
∴∠CBT+∠ABD=∠ABD+∠ABE=![]() ∠ABC,
∠ABC,
∴∠ABE=∠CBT,
∵BA=BC,
∴∠BAC=∠C,
∵∠BAE=∠BAC,
∴∠EAB=∠C,
在△BAE和△BCT中
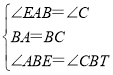
∴△BAE≌△BCT(ASA),
∴TC=AE,BE=BT,
在△DBE和△DBT中

∴△DBE≌△DBT(SAS),
∴DE=DT,
∴AE+DE=CT+DT=CD.
故答案为=.
(2)①结论:DE=CD+AE.
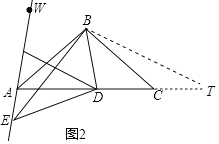
理由:如图2中,在AC的延长线上取一点T,使得∠TBD=![]() ∠ABC,连接BT.
∠ABC,连接BT.
∵∠TBD=![]() ∠ABC,∠DBE=50°=
∠ABC,∠DBE=50°=![]() ∠ABC,
∠ABC,
∴∠CBT+∠CBD=∠CBD+∠ABE=![]() ∠ABC,
∠ABC,
∴∠ABE=∠CBT,
∵BA=BC,
∴∠BAC=∠ACB,
∵∠BAE=∠BAC,
∴∠WAB=∠ACB,
∴∠BAE=∠BCT,
在△BAE和△BCT中
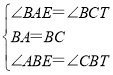
∴△BAE≌△BCT(ASA),
∴TC=AE,BE=BT,
在△DBE和△DBT中

∴△DBE≌△DBT(SAS),
∴DE=DT,
∴DE=DC+CT=AE+CD.
②由①可知:S△ABE=S△BCT,S△BDE=S△BDT,
∵S四边形ABDE﹣S△BCD=6,
∴S△BDC+2S△BCT﹣S△BDC=6,
∴S△BCT=3,
∵2DE=5AE,AD=![]() AE,设DE=5k,AE=2k,则AD=
AE,设DE=5k,AE=2k,则AD=![]() k,CD=DT﹣CT=DE﹣AE=3k,
k,CD=DT﹣CT=DE﹣AE=3k,
∴AC=AD+CD=![]() k+3k=
k+3k=![]() k,
k,
∴AC:CT=67:18,
∴S△ABC=![]() ×S△CBT=
×S△CBT=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形
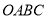 的边
的边 在数轴上,
在数轴上, 为原点,长方形
为原点,长方形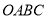 的面积为12,
的面积为12,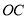 边的长为3.
边的长为3. 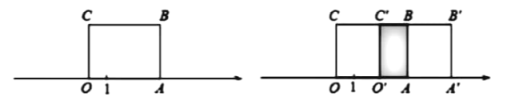
(1)数轴上点
 表示的数为________.
表示的数为________.(2)将长方形
 沿数轴水平移动,移动后的长方形记为
沿数轴水平移动,移动后的长方形记为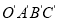 ,设长方形
,设长方形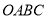 移动的距离为
移动的距离为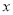 ,移动后的长方形
,移动后的长方形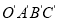 与原长方形
与原长方形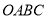 重叠部分的面积记为
重叠部分的面积记为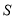 .
.①当
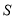 等于原长方形
等于原长方形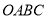 面积的
面积的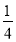 时,则点
时,则点 的移动距离
的移动距离 _______,此时数轴上点
_______,此时数轴上点 表示的数为_______.
表示的数为_______.②
 为线段
为线段 的中点,点
的中点,点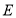 在线段
在线段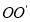 上,且
上,且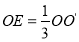 当点
当点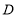 ,
,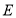 所表示的数互为相反数时,则
所表示的数互为相反数时,则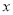 的值为_______.
的值为_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当
 ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)

-
科目: 来源: 题型:
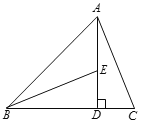
查看答案和解析>>【题目】已知:如图,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.
⑴ 求证:∠BED=∠C;
⑵ 若AC=13,DC=5,求AE的长.
-
科目: 来源: 题型:
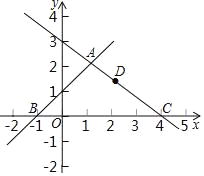
查看答案和解析>>【题目】如图,在平面直角坐标系可中,直线y=x+1与y=﹣
 x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出
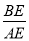 的值,不存在请说明理由;
的值,不存在请说明理由;(3)当△CBD为等腰三角形时直接写出D坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下结论:①单项式﹣
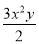 的系数为﹣
的系数为﹣ ,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+
,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+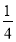 )﹣2(x﹣
)﹣2(x﹣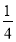 )的结果是﹣x+
)的结果是﹣x+ ;④若单项式
;④若单项式 ax2yn+1与﹣
ax2yn+1与﹣ axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
相关试题

