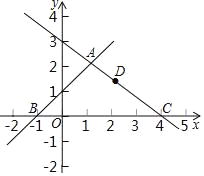
【题目】如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;
的值,不存在请说明理由;
(3)当△CBD为等腰三角形时直接写出D坐标.
参考答案:
【答案】(1)A(![]() ,
,![]() ),B(﹣1,0),C(4,0);(2)存在,
),B(﹣1,0),C(4,0);(2)存在,![]() =
=![]() ;(3)点D的坐标为(﹣
;(3)点D的坐标为(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).
【解析】
(1)将y=x+1与y=﹣![]() x+3联立求得方程组的解可得到点A的坐标,然后将y=0代入函数解析式求得对应的x的值可得到点B、C的横坐标;
x+3联立求得方程组的解可得到点A的坐标,然后将y=0代入函数解析式求得对应的x的值可得到点B、C的横坐标;
(2)当OE∥AD时,存在四边形EODA为平行四边形,然后依据平行线分线段成比例定理可得到![]() =
=![]() ;
;
(3)当DB=DC时,点D在BC的垂直平分线上可先求得点D的横坐标;即AC与y轴的交点为F,可求得CF=BC=F,当点D与点F重合或点D与点F关于点C对称时,三角形BCD为等腰三角形,当BD=BC时,设点D的坐标为(x,﹣![]() x+3),依据两点间的距离公式可知:(x+1)2+(﹣
x+3),依据两点间的距离公式可知:(x+1)2+(﹣![]() x+3)2=25,从而可求得点D的横坐标.
x+3)2=25,从而可求得点D的横坐标.
(1)将y=x+1与y=﹣![]() x+3联立得:
x+3联立得: ,
,
解得:x=![]() ,y=
,y=![]() ,
,
∴A(![]() ,
,![]() ).
).
把y=0代入y=x+1得:x+1=0,解得x=﹣1,
∴B(﹣1,0).
把y=0代入y=﹣![]() x+3得:﹣
x+3得:﹣![]() x+3=0,解得:x=4,
x+3=0,解得:x=4,
∴C(4,0).
(2)如图,存在点E使EODA为平行四边形.

∵EO∥AC,
∴![]() =
=![]() =
=![]() .
.
(3)当点BD=DC时,点D在BC的垂直平分线上,则点D的横坐标为![]() ,
,
将x=![]() 代入直线AC的解析式得:y=
代入直线AC的解析式得:y=![]() ,
,
∴此时点D的坐标为(![]() ,
,![]() ).
).
如图所示:
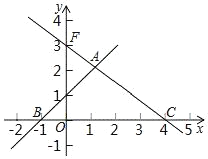
FC=![]() =5,
=5,
∴BC=CF,
∴当点D与点F重合时,△BCD为等腰三角形,
∴此时点D的坐标为(0,3);
当点D与点F关于点C对称时,CD=CB,
∴此时点D的坐标为(8,﹣3),
当BD=DC时,设点D的坐标为(x,﹣![]() x+3),
x+3),
依据两点间的距离公式可知:(x+1)2+(﹣![]() x+3)2=25,
x+3)2=25,
解得x=4(舍去)或x=﹣![]() ,
,
将x=﹣![]() 代入y=﹣
代入y=﹣![]() x+3得y=
x+3得y=![]() ,
,
∴此时点D的坐标为(﹣![]() ,
,![]() ).
).
综上所述点D的坐标为(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当
 ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)

-
科目: 来源: 题型:
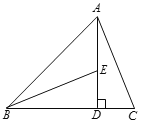
查看答案和解析>>【题目】已知:如图,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.
⑴ 求证:∠BED=∠C;
⑵ 若AC=13,DC=5,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,BA=BC,∠ABC=100°,AB平分∠WAC.在线段AC上有一动点D,连接BD并作∠DBE,使∠DBE=50°,BE边交直线AW于点E,连接DE.
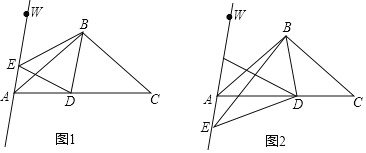
(1)如图1,当点E在射线AW上时,直接判断:AE+DE CD;(填“>”、“=”或“<”)
(2)如图2,当点E在射线AW的反向延长线上时,
①判断线段CD,DE,AE之间的数量关系,并证明;
②若S四边形ABDE﹣S△BCD=6,且2DE=5AE,AD=
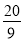 AE,求S△ABC的值.
AE,求S△ABC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下结论:①单项式﹣
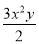 的系数为﹣
的系数为﹣ ,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+
,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+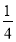 )﹣2(x﹣
)﹣2(x﹣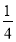 )的结果是﹣x+
)的结果是﹣x+ ;④若单项式
;④若单项式 ax2yn+1与﹣
ax2yn+1与﹣ axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
相关试题

