【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE= ![]() AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.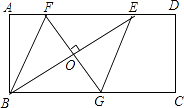
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1 , 矩形ABCD的面积为S2 , 当 ![]() =
= ![]() 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)
参考答案:
【答案】
(1)
解:∵AD∥BC,
∴∠EFO=∠BGO,
∵FG为BE的垂直平分线,
∴BO=OE;
∵在△EFO和△BGO中, 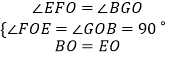 ,
,
∴△EFO≌△BGO,
∴FO=GO
∵EO=BO,且BE⊥FG
∴四边形BGEF为菱形.
(2)
解:当AB=a,n=3时,AD=2a,AE= ![]() ,
,
根据勾股定理可以计算BE= ![]() ,
,
∵AF=AE﹣EF=AE﹣BF,在Rt△ABF中AB2+AF2=BF2,计算可得AF= ![]() ,EF=
,EF= ![]() ,
,
∵菱形BGEF面积= ![]() BEFG=EFAB,计算可得FG=
BEFG=EFAB,计算可得FG= ![]()
(3)
解:设AB=x,则DE= ![]() ,
,
S1=BGAB,S2=BCAB
当 ![]() =
= ![]() 时,
时, ![]() =
= ![]() ,可得BG=
,可得BG= ![]() ,
,
在Rt△ABF中AB2+AF2=BF2,计算可得AF= ![]() ,
,
∴AE=AF+FE=AF+BG= ![]() ,DE=AD﹣AE=
,DE=AD﹣AE= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴n=6.
【解析】(1)先求证△EFO≌△BGO,可得FO=GO,再根据对角线互相垂直且平分的四边形是菱形,即可证明四边形BFEG为菱形;(2)根据菱形面积不同的计算公式(底乘高和对角线乘积的一半两种计算方式)可计算FG的长度;(3)根据菱形面积底乘高的计算方式可以求出BG长度,根据勾股定理可求出AF的长度,即可求出ED的长度,即可计算n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60,得到△BAE,连接ED,若BC=5,BD=4,则有以下四个结论:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC。其中正确结论的序号是( )
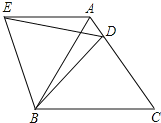
A. ②③④ B. ①③④ C. ①②④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=﹣
 的函数交于A(﹣2,b),B两点.
的函数交于A(﹣2,b),B两点. 
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值. -
科目: 来源: 题型:
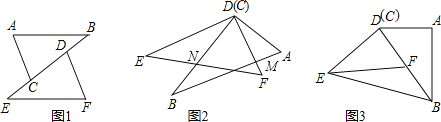
查看答案和解析>>【题目】如图1所示,已知在△ABC和△DEF中,AB=EF,∠B=∠E,EC=BD
(1)试说明:△ABC≌△FED;
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25°,∠A=66°,试求∠AMD的度数;
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE.请说明EF平分∠AED.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图,下列说法正确的有( )
①同一平面内,过点A有且只有一条直线AC垂直于直线l;②线段AB,AC,AD中,AC最短,根据是“两点之间的所有连线中,线段最短”;③线段AB,AC,AD中,AC最短,根据是“直线外一点,与直线上各点连接的所有线段中,垂线段最短”;④线段AC的长是点A到直线l的距离.

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

