【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=﹣ ![]() 的函数交于A(﹣2,b),B两点.
的函数交于A(﹣2,b),B两点. 
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
参考答案:
【答案】
(1)解:把A(﹣2,b)代入y=﹣ ![]() 得b=﹣
得b=﹣ ![]() =4,
=4,
所以A点坐标为(﹣2,4),
把A(﹣2,4)代入y=kx+5得﹣2k+5=4,解得k= ![]() ,
,
所以一次函数解析式为y= ![]() x+5
x+5
(2)解:将直线AB向下平移m(m>0)个单位长度得直线解析式为y= ![]() x+5﹣m,
x+5﹣m,
根据题意方程组  只有一组解,
只有一组解,
消去y得﹣ ![]() =
= ![]() x+5﹣m,
x+5﹣m,
整理得 ![]() x2﹣(m﹣5)x+8=0,
x2﹣(m﹣5)x+8=0,
△=(m﹣5)2﹣4× ![]() ×8=0,解得m=9或m=1,
×8=0,解得m=9或m=1,
即m的值为1或9
【解析】(1)先利用反比例函数解析式y=﹣ ![]() 求出b=4,得到A点坐标为(﹣2,4),然后把A点坐标代入y=kx+5中求出k,从而得到一次函数解析式为y=
求出b=4,得到A点坐标为(﹣2,4),然后把A点坐标代入y=kx+5中求出k,从而得到一次函数解析式为y= ![]() x+5;(2)由于将直线AB向下平移m(m>0)个单位长度得直线解析式为y=
x+5;(2)由于将直线AB向下平移m(m>0)个单位长度得直线解析式为y= ![]() x+5﹣m,则直线y=
x+5﹣m,则直线y= ![]() x+5﹣m与反比例函数有且只有一个公共点,即方程组
x+5﹣m与反比例函数有且只有一个公共点,即方程组  只有一组解,然后消去y得到关于x的一元二次函数,再根据判别式的意义得到关于m的方程,最后解方程求出m的值.
只有一组解,然后消去y得到关于x的一元二次函数,再根据判别式的意义得到关于m的方程,最后解方程求出m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

-
科目: 来源: 题型:
查看答案和解析>>【题目】第十五届中国“西博会”将于2014年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;
(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60,得到△BAE,连接ED,若BC=5,BD=4,则有以下四个结论:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC。其中正确结论的序号是( )
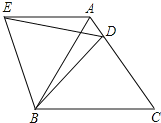
A. ②③④ B. ①③④ C. ①②④ D. ①②③
-
科目: 来源: 题型:
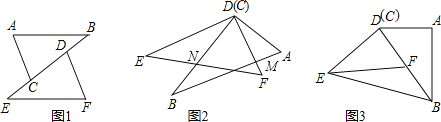
查看答案和解析>>【题目】如图1所示,已知在△ABC和△DEF中,AB=EF,∠B=∠E,EC=BD
(1)试说明:△ABC≌△FED;
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25°,∠A=66°,试求∠AMD的度数;
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
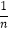 AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.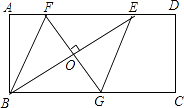
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1 , 矩形ABCD的面积为S2 , 当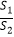 =
= 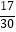 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
相关试题

