【题目】(1)如图1,在![]() 中,分别以
中,分别以![]() 、
、![]() 为斜边,向
为斜边,向![]() 的形外作等腰直角三角形,直角的顶点分别为
的形外作等腰直角三角形,直角的顶点分别为![]() ,点
,点![]() 分别为
分别为![]() 边的中点.问:
边的中点.问: ![]() 是否全等?____(填“是”或“否”);
是否全等?____(填“是”或“否”);
(2)如图2,在![]() 中,分别以
中,分别以![]() 为底边,向
为底边,向![]() 的形外作等腰三角形,顶角的顶点分别为
的形外作等腰三角形,顶角的顶点分别为![]() ,且
,且![]() .点
.点![]() 分别为
分别为![]()
![]() 边的中点.
边的中点.
①试判断![]() 是否满足(1)中的关系?若满足,请说明理由;若不满足,请写
是否满足(1)中的关系?若满足,请说明理由;若不满足,请写![]() 之间存在的一种关系,并加以说明.
之间存在的一种关系,并加以说明.
②若![]() ,
, ![]() ,
, ![]() 的面积为32,求
的面积为32,求![]() 的面积.
的面积.

参考答案:
【答案】(1)是;(2)①否, ![]() 相似,理由见解析;②
相似,理由见解析;②![]() .
.
【解析】试题分析:
(1)由已知条件易证:DF=AF=GM,FM=AG=GE,∠DFB=∠EGC=90°,∠BFM=∠BAC=∠MGC,从而可得∠DFM=∠EGM,由此即可由“SAS”证得△DFM≌△MGE;
(2)①同(1)可证得∠DFM=∠MGE,由∠BAD+∠CAE=90°,结合∠AGE=90°,可证得∠DAF=∠AEG,从而可得tan∠DAF=tan∠AEG,由此可得![]() ,结合AF=GM,AG=FM可得
,结合AF=GM,AG=FM可得![]() ,这样即可证得△DFM∽△MGE了;
,这样即可证得△DFM∽△MGE了;
②由AB=6易得AF=MG=3,结合AD=5,在Rt△ADF中易得DF=4,从而可得DF:MG=4:3,结合△DFM∽△MGE即可由△DFM的面积求得△MGE的面积了.
试题解析:
(1)是,理由如下:
∵△ABD、△AEC分别是以AB和AC为斜边的等腰直角三角形,点F、M、G分别是AB、BC、AC的中点,
∴DF=AF=GM,FM=AG=GE,∠DFB=∠EGC=90°,FM∥AC,MG∥AB,
∴∠BFM=∠BAC=∠MGC,
∴∠DFB+∠BFM=∠MGC+∠EGC,即∠DFM=∠EGM,
∴△DFM≌△MGE;
故答案为:“是”;
(2)①否, ![]() 相似;
相似;
理由:∵![]() 都是等腰三角形,且
都是等腰三角形,且![]() 为
为![]() 的中点,
的中点,
∴![]() ,∵点
,∵点![]() 分别为
分别为![]() 边的中点,
边的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∵由①知![]() ,且
,且![]() 的面积为32,
的面积为32,
∴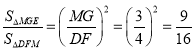 ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年9月12日,Apple(苹果公司)发布了iPhone X。苹果公司某生产车间计划平均每天生产iPhone X手机200台,但是由于种种原因,实际每天生产量与计划生产量相比有出入.下表是某周的生产情况(超产记为正,减产即为负)

(1)根据记录的数据可知该车间星期三生产iPhone X手机 台?
(2)产量最多的一天比产量最少的一天多生产iPhone X手机 台?
(3)根据记录的数据可知该车间本周实际共生产iPhone X手机多少台?(请写出解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数
1套至45套
46套至90套
91套以上
每套服装的价格
60元
50元
40元
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=
 x﹣8的解.
x﹣8的解.①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
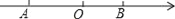
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则
 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 ,同理有:
,同理有:  ,所以
,所以 .
.即:在一个锐角三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)某次巡逻中,如图(3),我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政船距钓鱼岛A的距离AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初一年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.
(1)若有m名学生,用代数式表示两种优惠方案各需多少元?
(2)当m=70时,采用哪种方案优惠?
相关试题

