【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有: ![]() ,所以
,所以![]() .
.
即:在一个锐角三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)某次巡逻中,如图(3),我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政船距钓鱼岛A的距离AB.
参考答案:
【答案】(1)60°,20![]() ;(2)10
;(2)10![]()
【解析】试题分析:(1)先利用三角形内角和定理求出∠A,再利用题目总结的正弦定理,将有关数据代入求解即可;
(2)在△ABC中,分别求得BC的长和三个内角的度数,利用题目中总结的正弦定理AB的长即可.
试题解析:(1)∵∠B=45°,∠C=75°,∴∠A=180°-∠B-∠C=60°,
根据材料有: ![]() ,∴
,∴![]() ,即
,即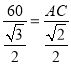 ,∴AC=20
,∴AC=20![]() ,
,
故答案为:60°,20![]() ;
;
(2)如图,依题意:BC=40×0.5=20(海里),
∵CD∥BE,∴∠DCB+∠CBE=180°.∵∠DCB=30°,∴∠CBE=150°,
∵∠ABE=75°,∴∠ABC=75°,∴∠A=45°,
在△ABC中, ![]() , 即
, 即![]() , 解之得:AB=10
, 解之得:AB=10![]() 海里,
海里,
所以渔政船距钓鱼岛A的距离为10![]() 海里.
海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在
 中,分别以
中,分别以 、
、 为斜边,向
为斜边,向 的形外作等腰直角三角形,直角的顶点分别为
的形外作等腰直角三角形,直角的顶点分别为 ,点
,点 分别为
分别为 边的中点.问:
边的中点.问:  是否全等?____(填“是”或“否”);
是否全等?____(填“是”或“否”);(2)如图2,在
 中,分别以
中,分别以 为底边,向
为底边,向 的形外作等腰三角形,顶角的顶点分别为
的形外作等腰三角形,顶角的顶点分别为 ,且
,且 .点
.点 分别为
分别为
 边的中点.
边的中点.①试判断
 是否满足(1)中的关系?若满足,请说明理由;若不满足,请写
是否满足(1)中的关系?若满足,请说明理由;若不满足,请写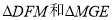 之间存在的一种关系,并加以说明.
之间存在的一种关系,并加以说明.②若
 ,
,  ,
,  的面积为32,求
的面积为32,求 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=
 x﹣8的解.
x﹣8的解.①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
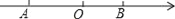
-
科目: 来源: 题型:
查看答案和解析>>【题目】初一年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.
(1)若有m名学生,用代数式表示两种优惠方案各需多少元?
(2)当m=70时,采用哪种方案优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级所有学生参加2015年初中毕业生升学体育测试,为了解情况,从中抽取了部分学生的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)计算一共抽取了多少名学生的测试成绩并将条形统计图补充完整;
(2)在扇形统计图中,等级C对应的圆心角的度数为多少度?
(3)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=x+m的图象与反比例函数
 的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
(1)求一次函数的解析式;
(2)已知双曲线在第一象限上有一点C到y轴的距离为3,求△ABC的面积.
相关试题

