【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

参考答案:
【答案】(1)猜想:OE=OF,理由见解析;(2)见解析;(3)见解析.
【解析】
(1)猜想:OE=OF,由已知MN∥BC,CE、CF分别平分∠BCO和∠GCO,可推出∠OEC=∠OCE,∠OFC=∠OCF,所以得EO=CO=FO.
(2)由(1)得出的EO=CO=FO,点O运动到AC的中点时,则由EO=CO=FO=AO,所以这时四边形AECF是矩形.
(3)由已知和(2)得到的结论,点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,则推出四边形AECF是矩形且对角线垂直,所以四边形AECF是正方形.
(1)猜想:OE=OF,理由如下:
∵MN∥BC,∴∠OEC=∠BCE,∠OFC=∠GCF,
又∵CE平分∠BCO,CF平分∠GCO,∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,∴EO=CO,FO=CO,∴EO=FO.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,∴四边形AECF是平行四边形,
∵FO=CO,∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,∴四边形AECF是矩形.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,∴AC⊥EF,∴四边形AECF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
-
科目: 来源: 题型:
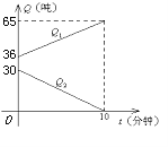
查看答案和解析>>【题目】某军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油的过程中,设运输飞机的油箱余油量为Q1吨,加油飞机的加油油箱的余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数关系如图.回答问题:
(1) 加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?
(2) 求加油过程中,运输飞机的余油量Q1(吨)与时间t(分钟)的函数关系式;
(3) 运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?
请通过计算说明理由.
-
科目: 来源: 题型:
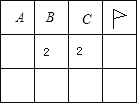
查看答案和解析>>【题目】Windows2000下有一个有趣的游戏“扫雷”,下图是扫雷游戏的一部分:(说明:图中数字2表示在以该数字为中心的8个方格中有2个地雷).小旗表示该方格已被探明有地雷,现在还剩下A、B、C三个方格未被探明,其它地方为安全区(包括有数字的方格)
(1)现在还剩下几个地雷?
(2)A、B、C三个方格中有地雷的概率分别是多大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
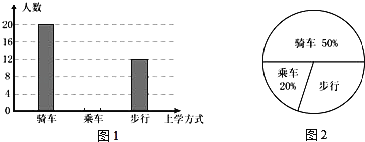
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将5张都是10元的纸币随机装入10个完全相同的信封中,设计以下几种抽奖游戏:
(1)游戏A:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为
 ;
;(2)游戏B:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为
 .
. -
科目: 来源: 题型:
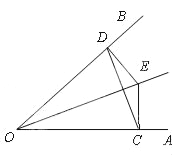
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D.
(1)请判断△EDC的形状并说明理由;
(2)求证OE是线段CD的垂直平分线.
相关试题

