【题目】阅读下列解题过程:已知![]() 、
、![]() 、
、![]() 为△ABC的三边,且满足
为△ABC的三边,且满足![]() ,
,
试判断△ABC的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴△ABC为直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号________;
(2)错误的原因是____________________________;
(3)本题的正确结论是_________________________.
参考答案:
【答案】 (1)③; (2)没有考虑![]() 的情况; (3)△ABC为直角三角形或等腰三角形或等腰直角三角形.
的情况; (3)△ABC为直角三角形或等腰三角形或等腰直角三角形.
【解析】整体分析:
等式两边同时除以同一个式子时,要注意这个式子是否能够为0,要注意xy=0的意义是x,y至少有一个为0.
解:(1)从②到③时,等式两边同时除以了![]() ,但
,但![]() 有可能为0,所以第③步开始出现错误,错误代号为③,故答案为③;
有可能为0,所以第③步开始出现错误,错误代号为③,故答案为③;
(2)等式两边同时除以一个数或式子时,这个数或式子不能为0,但![]() 有可能为0,故答案为没有考虑
有可能为0,故答案为没有考虑![]() 的情况
的情况
(3)∵![]() ,
,
∴![]() ,
,
∴(![]() )(
)(![]() )=0,
)=0,
∴![]() =0或
=0或![]() =0,
=0,
则△ABC为直角三角形或等腰三角形或等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”“科学实验”“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
某校被调查学生选择社团意向统计表
选择意向
文学鉴赏
科学实验
音乐舞蹈
手工编织
其他
所占百分比
a
35%
b
10%
c

根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整.
-
科目: 来源: 题型:
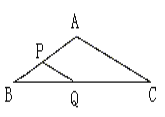
查看答案和解析>>【题目】如图,在△ABC中(∠B≠∠C),AB=8 cm,BC=16 cm,点P从点A开始沿边AB向点B以2 cm/s的速度移动,点Q从点B开始沿边BC向点C以4 cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(庆阳中考)现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了了解学生的视力变化情况,从全市九年级随机抽取了1 500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
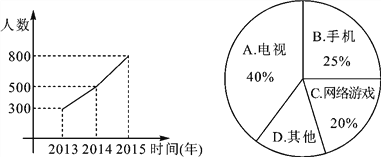
解答下列问题:
(1)图中D所在扇形的圆心角度数为______;
(2)若2016年全市共有30 000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的重量(kg)之间的关系如下表:
所挂物体的重量(kg)
0
1
2
3
4
5
6
7
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
15
15.5
(1)当所挂物体的重量为3kg时,弹簧的长度是_____________cm;
(2)如果所挂物体的重量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的重量为5.5kg时,请求出弹簧的长度。
(4)如果弹簧的最大伸长长度为20cm,则该弹簧最多能挂多重的物体?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向
 点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻
点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻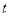 ,使以A,M,N为顶点的三角形与△ACD相似?若存在,求
,使以A,M,N为顶点的三角形与△ACD相似?若存在,求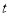 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.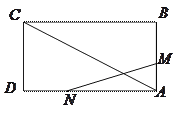
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若
 ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:(1)试说明
 ;
;(2)如果大正方形的面积是10,小正方形的面积是2,求
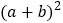 的值.
的值.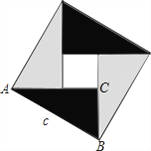
相关试题

