【题目】已知线段![]() 和线段
和线段![]() .
.

(1)按要求作图(保留作围痕迹,不写作法);
延长线段![]() 至点
至点![]() ,使
,使![]() ,反向延长线段
,反向延长线段![]() 至点
至点![]() ,使
,使![]() ;
;
(2)如果![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)延长AB,以B为圆心,以AB长度为半径画弧,与AB延长线交点即为C,延长BA,以A为圆心,以a为半径画弧,交BA延长线于点E,再以E为圆心,以a为半径画弧,交BA延长线于点D即可.
(2)根据题意和(1)中结论,可得AD、AB、BC的长度,再根据![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,求出DM和DN的长,即可得MN的长.
的中点,求出DM和DN的长,即可得MN的长.
解:(1)如图,即为所作图形:

(2)如图,∵a=2,AB=3,
∴AD=4,AB=BC=3,
∵![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,
的中点,
∴DN=CD,DM=AD+AM,
∵CD=AD+AB+BC=10,DM=AD+![]() AB=5.5,
AB=5.5,
∴MN=DM-DN=5.5-![]() CD=0.5=
CD=0.5=![]() .
.
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】蚌埠云轨测试线自开工以来备受关注,据了解我市首期工程云轨线路约12千米,若该任务由甲、乙两工程队先后接力完成,甲工程队每天修建
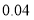 千米,乙工程队每天修建
千米,乙工程队每天修建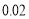 千米,两工程队共需修建500天,求甲、乙两工程队分别修建云轨多少千米?
千米,两工程队共需修建500天,求甲、乙两工程队分别修建云轨多少千米?根据题意,小刚同学列出了一个尚不完整的方程组:
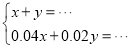
(1)根据小刚同学所列的方程组,请你分别指出未知数
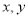 表示的意义.
表示的意义.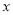 表示____________;
表示____________;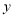 表示________________.
表示________________.(2)小红同学“设甲工程队修建云轨
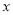 千米,乙工程队修建云轨
千米,乙工程队修建云轨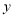 千米”请你利用小红同学设的未知数解决问题.
千米”请你利用小红同学设的未知数解决问题. -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上有两个动点M,N,如果点M始终在点N的左侧,我们称作点M是点N的“追赶点”.如图,数轴上有2个点A,B,它们表示的数分别为-3,1,已知点M是点N的“追赶点”,且M,N表示的数分别为m,n.
(1)由题意得:点A是点B的“追赶点”,AB=1-(-3)=4(AB表示线段AB的长,以下相同);类似的,MN=____________.
(2)在A,M,N三点中,若其中一个点是另外两个点所构成线段的中点,请用含m的代数式来表示n.
(3)若AM=BN,MN=
 BM,求m和n值.
BM,求m和n值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一直角三角板
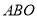 的直角顶点
的直角顶点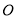 在直线
在直线 上,作射线
上,作射线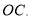 三角板的各边和射线
三角板的各边和射线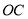 都处于直线
都处于直线 的上方.
的上方.
(1)将三角板绕
 点在平面内旋转,当
点在平面内旋转,当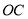 平分
平分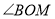 时,如图1,如果
时,如图1,如果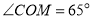 ,求
,求 的度数;
的度数;(2)如图2,将三角板
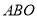 绕
绕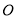 点在平面内任意转动,如果
点在平面内任意转动,如果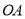 始终在
始终在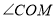 内,且
内,且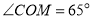 ,请问:
,请问: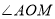 和
和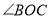 有怎样的数量关系?
有怎样的数量关系?(3)如图2,如果
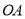 平分
平分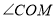 ,
,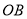 是否也平分
是否也平分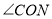 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段话,并解决后面的问题 .观察下面一例数:
1,2,4,8,……
我们发现,这一列数从第2项起,每一项与它前一项的比都等于2 .
一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比 .
(1)等比数列5,-15,45,……的第4项是 ;
(2)如果一列数
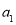 ,
,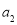 ,
,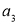 ,
,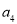 ,……是等比数列,且公比为q,那么根据上述的规定,有
,……是等比数列,且公比为q,那么根据上述的规定,有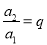 ,
,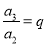 ,
,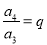 ,……
,……所以
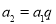 ,
,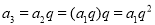 ,
,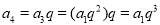 ,
,……
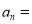 .(用
.(用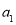 与q的代数式表示)
与q的代数式表示)(3)一个等比数列的第2项是10,第3项是20,求它的第1项与第4项 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设国家森林城市,园林部门决定搭配A.B两种园艺造型共50个摆放在市区,现有3490盆甲种花卉和2950盆乙种花卉可供使用,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的费用是800元,搭配一个B种造型的费用是960元,试说明(1)中哪种方案费用最低?最低费用是多少元?
相关试题

