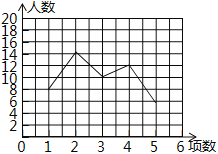
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
参考答案:
【答案】(1)被随机抽取的学生共有50人;(2)活动数为3项的学生所对应的扇形圆心角为72°,(3)参与了4项或5项活动的学生共有720人.
【解析】(1)利用活动数为2项的学生的数量以及百分比,即可得到被随机抽取的学生数;
(2)利用活动数为3项的学生数,即可得到对应的扇形圆心角的度数,利用活动数为5项的学生数,即可补全折线统计图;
(3)利用参与了4项或5项活动的学生所占的百分比,即可得到全校参与了4项或5项活动的学生总数.
(1)被随机抽取的学生共有14÷28%=50(人);
(2)活动数为3项的学生所对应的扇形圆心角=![]() ×360°=72°,
×360°=72°,
活动数为5项的学生为:50﹣8﹣14﹣10﹣12=6,
如图所示:
(3)参与了4项或5项活动的学生共有![]() ×2000=720(人).
×2000=720(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
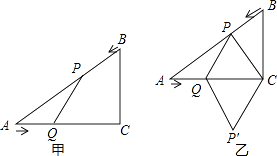
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数
 ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
-
科目: 来源: 题型:
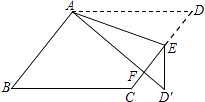
查看答案和解析>>【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:

(1)抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.
(2)若学校有600名学生,请估计该校训练后成绩为“A”等次的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.

(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是(用树状图或列表法求解).
相关试题

