【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分100分)分成四类,并制作了如下的统计图表:
类别 | 甲 | 乙 | 丙 | 丁 |
成绩 | 60≤m<70 | 70≤m<80 | 80≤m<90 | 90≤m<100 |
频数 | 5 | 10 | a | b |
根据图表信息,回答下列问题:
(1)该班共有学生 人,表中a= ,b= ;
(2)扇形图中,丁类所对应的圆心角是 度;
(3)已知A同学在丁类中,现从丁类同学中随机抽两名同学参加学校的决赛,请用列举的方法求A同学能够参加决赛的概率.

参考答案:
【答案】(1)、40,20,5;(2)、45°;(3)、![]() .
.
【解析】
试题分析:(1)、用乙类的人数除一它所占的百分比即可得到调查的学生总数,再利用学生总数乘以丙类所占的百分比得到a的值,然后用学生总数分别减去甲乙丙类的人数得到b的值;(2)、丁类所对应的圆心角等于丁类的所占的百分比乘以360°;(3)、设丁类的5个同学分别用A、B、C、D、E表示,画树状图展示所有20种等可能的结果数,再找出A同学能够参加决赛的结果数,然后根据概率公式求解.
试题解析:(1)、调查的学生总数=10÷25%=40(人), 所以a=40×50%=20,b=40﹣5﹣10﹣20=5;
(2)、丁类所对应的圆心角=360°×![]() =45°; (3)、设丁类的5个同学分别用A、B、C、D、E表示,
=45°; (3)、设丁类的5个同学分别用A、B、C、D、E表示,
画树状图为:
共有20种等可能的结果数,其中A同学能够参加决赛的结果数为8,
所以A同学能够参加决赛的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
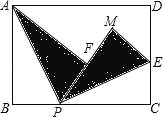
查看答案和解析>>【题目】如图,矩形纸片ABCD的边AB=3,BC=4,点P是BC边上一动点(不与B、C重合),现将△ABP沿AP翻折,得到△AFP,再在CD边上选择适当的点E,将△PCE沿PE翻折,得到△PME,且直线PF、PM重合,若点F落在矩形纸片的内部,则CE的最大值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于 2 且不大于 4 的所有整数的积是_____,和是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国研制的高性能计算机“曙光3000超级服务器”,它的峰值速度达到每秒403200000000次,用科学记数法表示它的峰值计算速度为每秒___________次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3b﹣ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3+a3=2a6
B.a6÷a﹣3=a3
C.a3a3=2a3
D.(﹣2a2)3=﹣8a6 -
科目: 来源: 题型:
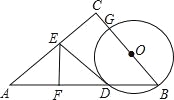
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AB=10,cosB=
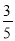 ,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.
,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.(1)求证:DE为⊙O的切线;
(2)若BG=3,求DE的长;
(3)设BG=x,DE=y,求y与x的函数关系,写出y的最小值.
相关试题

