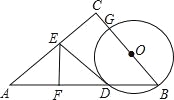
【题目】如图,在△ABC中,∠ACB=90°,AB=10,cosB=![]() ,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.
,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.
(1)求证:DE为⊙O的切线;
(2)若BG=3,求DE的长;
(3)设BG=x,DE=y,求y与x的函数关系,写出y的最小值.
参考答案:
【答案】(1)、证明过程见解析;(2)、![]() ;(3)、y与x的函数关系是y=
;(3)、y与x的函数关系是y=![]() ,(0<x≤6),y的最小值是4.
,(0<x≤6),y的最小值是4.
【解析】
试题分析:(1)、连接OD、DG,由BG为圆的直径可知∠BDG是直角,然后只要证明∠ODE=90°,即可证明结论成立,根据题目中的条件可以得到∠ODE=90°,本题得以解决;(2)、根据题目中的条件和勾股定理,可以转化为直角三角形ODE和直角三角形OCD两直角边的平方等于OE的平方,从而可以得到DE的长;(3)、根据(2)中的求解方法,可以得到y与x的函数关系式,根据一次函数的性质,可以得到y的最小值.
试题解析:(1)、连接OD、DG,如右图所示, ∵BG为⊙O的直径,OD=OB,∠ACB=90°,
∴∠BDG=90°,∠ODB=∠B,∠B+∠A=90°, ∴∠A=∠ODG,∠GDE+∠EDA=90°,
又∵EF是AD的垂直平分线, ∴∠A=∠EDA, ∴∠EDA=∠ODG, ∴∠GDE+∠ODG=90°,
即OD⊥DE, ∵OD是⊙O的半径, ∴DE为⊙O的切线;
(2)、连接OE,如右上图所示,
∵∠ACB=90°,AB=10,cosB=![]() , ∴BC=ABcosB=6,AC=8, ∵BG=3,
, ∴BC=ABcosB=6,AC=8, ∵BG=3,
∴OD=1.5,OC=BC﹣OB=6﹣1.5=4.5, ∵EF是AD的垂直平分线, ∴EA=ED,
设EA=x,则ED=x,EC=8﹣x, ∵∠ECO=90°,∠EDO=90°, ∴DE2+OD2=EC2+OC2,
即x2+1.52=(8﹣x)2+4.52, 解得,x=![]() , 即DE的长是
, 即DE的长是![]() ;
;
(3)、连接OE,如右上图所示,
∵∠ACB=90°,AB=10,cosB=![]() , ∴BC=ABcosB=6,AC=8, ∵BG=x,
, ∴BC=ABcosB=6,AC=8, ∵BG=x,
∴OD=0.5x,OC=BC﹣OB=6﹣0.5x, ∵EF是AD的垂直平分线,ED=y, ∴EA=ED=y, ∴EC=8﹣y,
∵∠ECO=90°,∠EDO=90°, ∴DE2+OD2=EC2+OC2, 即y2+(0.5x)2=(8﹣y)2+(6﹣0.5x)2,
化简,得y=![]() ,(0<x≤6) ∵﹣
,(0<x≤6) ∵﹣![]() <0, ∴y随x的增大而减小,
<0, ∴y随x的增大而减小,
∴当x=6时,y取得最小值,此时y=![]() =4, 即y与x的函数关系是y=
=4, 即y与x的函数关系是y=![]() ,(0<x≤6),y的最小值是4.
,(0<x≤6),y的最小值是4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分100分)分成四类,并制作了如下的统计图表:
类别
甲
乙
丙
丁
成绩
60≤m<70
70≤m<80
80≤m<90
90≤m<100
频数
5
10
a
b
根据图表信息,回答下列问题:
(1)该班共有学生 人,表中a= ,b= ;
(2)扇形图中,丁类所对应的圆心角是 度;
(3)已知A同学在丁类中,现从丁类同学中随机抽两名同学参加学校的决赛,请用列举的方法求A同学能够参加决赛的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3b﹣ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3+a3=2a6
B.a6÷a﹣3=a3
C.a3a3=2a3
D.(﹣2a2)3=﹣8a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据3,x,4,5,8的平均数为5,则这组数据的众数、中位数分别是( )
A.4,5
B.5,5
C.5,6
D.5,8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)若x1、x2满足|x1|+|x2|=2|x1x2|﹣3,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x+y﹣3)2+|5+xy|=0,则x﹣xy+y=______.
相关试题

