【题目】如图,ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F.
(1)求证:AF=DE;
(2)若E为AD的三等分点(靠近A点),BE=8,CF=6,求直线AD与BC之间的距离.

参考答案:
【答案】(1)见解析 (2)4.8
【解析】
(1)证出∠AEB=∠ABE,∠DFC=∠DCF,得出AE=AB,DF=DC,得出AE=DF,进而得出结论;
(2)作EM⊥BC于M,证出AE=EF=DF,过点E作EP∥CF交BC于P,则∠BPE=∠BCF,四边形CFEP是平行四边形,得出EP=CF=6,证出∠BEP=90°,由勾股定理求出![]() ,由面积法求出
,由面积法求出![]() 即可.
即可.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,AD∥BC,
∴∠AEB=∠CBE,∠DFC=∠BCF,
∵BE平分∠ABC,CF平分∠BCD.
∴∠ABE=∠CBE,∠DCF=∠BCF,
∴∠AEB=∠ABE,∠DFC=∠DCF,
∴AE=AB,DF=DC,
∴AE=DF,
∴AE+EF=DF+EF,
即AF=DE;
(2)解:作EM⊥BC于M,如图所示:
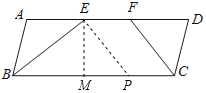
由(1)得:AE=DF,
∵E为AD的三等分点,
∴AE=EF=DF,
过点E作EP∥CF交BC于P,
则∠BPE=∠BCF,四边形CFEP是平行四边形,
∴EP=CF=6,
∵AB∥DC,
∴∠ABC+∠DCB=180°,
∵BE平分∠ABC,CF平分∠BCD.
∴∠ABE=∠CBE,∠DCF=∠BCF,
∴∠CBE+∠BCF=90°,
∴∠CBE+∠BPE=90°,
∴∠BEP=90°,
∴![]() ,
,
∴![]() ,
,
即AD与BC之间的距离为4.8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体由大小相同的正方体搭成,从上面看到的几何体的形的形状状图如图所示,其中小正方形中的数字表示在该位置的小正方体的个数,

(1)请画出从正面和左面看到的这个几何体的形状图.
(2)若每个小正方图的棱长都为1,则搭成的这个几何体的体积为 .
-
科目: 来源: 题型:
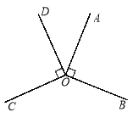
查看答案和解析>>【题目】如图,∠AOB=∠COD=90°
(1)∠AOC和∠BOD的大小有什么关系?请说明理由.
(2)若∠BOD=150°,则∠BOC是多少度?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD,其中正确的有( )

A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完整.

解:∵EF∥AD(已知),
∴∠2=________(________________________).
又∵∠1=∠2(____________),
∴∠1=_____(____________).
∴AB∥________(________________________).
∴∠DGA+∠BAC=180°(______________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果过三角形一个顶点的直线与对边所在直线相交,得到的三角形中有一个与原三角形相似,那么我们称这样的直线为三角形的相似线.
如图1,△ABC中,直线CD与AB交于点D,若△ACD∽△ABC,则称直线CD是△ABC的相似线.

解决问题:
已知:如图2,在△ABC中,∠BAC>∠ACB >∠ABC.
求作:△ABC的相似线.

(1)小明用如下方法作出△ABC的一条相似线:
作法:如图3,①作△ABC的外接圆⊙O;
②以C为圆心,AC的长为半径画弧,与⊙O交于点P;
③连接AP,交BC于点D.
则直线AD为△ABC的相似线.
请你证明小明的作法的正确性.
(2)过A点还有其它的△ABC的相似线,请你参考(1)中的作法与结论,利用尺规作图,在图3中再作出一条△ABC的相似线AE;(写出作法,保留作图痕迹,不要证明)
(3)若△ABC中,∠BAC=90°,则△ABC中过A点的相似线有 条,过B点的相似线有 条.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC.
(1)求证:AC平分∠BAD;
(2)若AB=6,AC=4
 ,求EC和PB的长.
,求EC和PB的长.
相关试题

