【题目】某商场计划用![]() 元从厂家购进
元从厂家购进![]() 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入![]() 台,其中每台的价格、销售获利如下表:
台,其中每台的价格、销售获利如下表:
甲型 | 乙型 | 丙型 | |
价格(元/台) |
|
|
|
销售获利(元/台) |
|
|
|
![]() 购买丙型设备 台(用含
购买丙型设备 台(用含![]() 的代数式表示) ;
的代数式表示) ;
![]() 若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了![]() 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?
![]() 在第
在第![]() 题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
参考答案:
【答案】(1) ![]() ; (2) 购进方案有三种,分别为:方案一:甲型
; (2) 购进方案有三种,分别为:方案一:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;方案二:甲型
台;方案二:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;方案三:甲型
台;方案三:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;(3) 购进甲型
台;(3) 购进甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台,获利最多,为
台,获利最多,为![]() 元
元
【解析】
(1)用总台数减去甲、乙两型的数量及得丙的数量;
(2)根据总费用恰好是56000元可列写一个等式方程,其中包含2个未知数,仅能得出x、y之间的关系式:![]() .再利用x、y都是正数,可得y必须是5的倍数;
.再利用x、y都是正数,可得y必须是5的倍数;
(3)在(2)中得出的几种方案中,分别求解利润,得出利润最多的情况
解:![]()
![]() 由题意得,
由题意得,![]()
化简整理得:![]()
![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
![]() 购进方案有三种,分别为:
购进方案有三种,分别为:
方案一:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;
台;
方案二:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;
台;
方案三:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台.
台.
![]() 方案一:
方案一:![]() (元),故可获利
(元),故可获利![]() 元,
元,
方案二一:![]() (元),故可获利
(元),故可获利![]() 元,
元,
方案三:![]() (元),故可获利
(元),故可获利![]() 元,
元,
因为![]()
所以购进甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台,获利最多,为
台,获利最多,为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
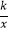 在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.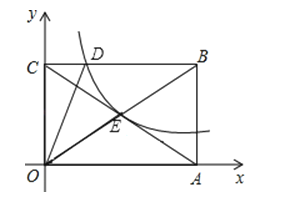
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.

解:∵AB∥CD(已知)
∴∠EFD=∠AEF( )
∵∠AEF=68°(已知)
∴∠EFD=∠AEF=68°( )
∵FG平分∠EFD(已知)
所以∠EFG=∠GFD=
 ∠EFD=34°( )
∠EFD=34°( )又因为KF⊥FG( )
所以∠KFG=90°( )
所以∠KFC=180°-∠GFD-∠KFG= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用完全平方公式进行因式分解,解答下列问题:
 因式分解:
因式分解: .
. 填空: ①当
填空: ①当 时,代数式
时,代数式 _ .
_ .②当
 _ 时,代数式
_ 时,代数式 .
.③代数式
 的最小值是_ .
的最小值是_ . 拓展与应用:求代数式
拓展与应用:求代数式 的最小值.
的最小值. -
科目: 来源: 题型:
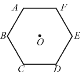
查看答案和解析>>【题目】如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O旋转多少度后能和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为
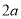 、宽为
、宽为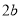 的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.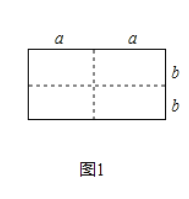
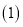 图2中的阴影部分的正方形的边长是 .
图2中的阴影部分的正方形的边长是 .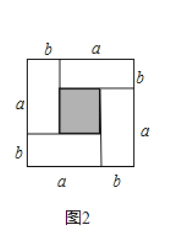
 请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:
请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式: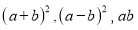 之间的等量关系;
之间的等量关系; 利用
利用 中的结论计算:
中的结论计算: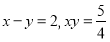 ,求
,求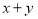 的值;
的值;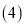 根据
根据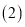 中的结论,直接写出
中的结论,直接写出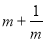 和
和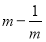 之间的关系;若
之间的关系;若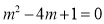 ,分别求出
,分别求出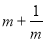 和
和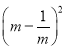 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
相关试题

