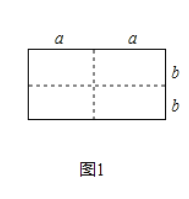
【题目】如图1是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
![]() 图2中的阴影部分的正方形的边长是 .
图2中的阴影部分的正方形的边长是 .
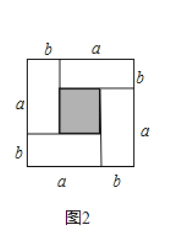
![]() 请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:
请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:![]() 之间的等量关系;
之间的等量关系;
![]() 利用
利用![]() 中的结论计算:
中的结论计算:![]() ,求
,求![]() 的值;
的值;
![]() 根据
根据![]() 中的结论,直接写出
中的结论,直接写出![]() 和
和![]() 之间的关系;若
之间的关系;若![]() ,分别求出
,分别求出![]() 和
和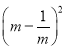 的值.
的值.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ;(4)4,12
;(4)4,12
【解析】
(1)图2中,大正方形的边长为:a+b,横着看,a+b是由两个b和阴影正方形的边长构成,相减便得阴影正方形边长;
(2)方法一:图1中已求出阴影正方形的边长,边长乘边长即为面积;方法二:图2长方形面积减图2非阴影部分面积,即为阴影部分面积‘’
(3)由(2)可得![]() 之间的关系,运用这个关系可直接求得x+y的值;
之间的关系,运用这个关系可直接求得x+y的值;
(4)将m视为a,![]() 视为b,按照上述结论即可解决
视为b,按照上述结论即可解决
解:(1)图2中,大正方形的边长为:a+b,
∴阴影正方形的边长=a+b-b-b=a-b
![]() 阴影部分面积可以表示为:
阴影部分面积可以表示为:![]() 和
和![]()
三个式子![]() 之间的等量关系:
之间的等量关系:![]()
![]() 由
由![]() 可知,
可知,![]()
![]()
![]() 根据
根据![]() 中的结论,可得
中的结论,可得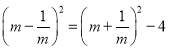
![]() 且
且![]() 不能为
不能为![]()
![]()
![]()
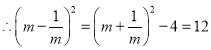
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用完全平方公式进行因式分解,解答下列问题:
 因式分解:
因式分解: .
. 填空: ①当
填空: ①当 时,代数式
时,代数式 _ .
_ .②当
 _ 时,代数式
_ 时,代数式 .
.③代数式
 的最小值是_ .
的最小值是_ . 拓展与应用:求代数式
拓展与应用:求代数式 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划用
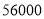 元从厂家购进
元从厂家购进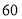 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入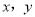 台,其中每台的价格、销售获利如下表:
台,其中每台的价格、销售获利如下表:甲型
乙型
丙型
价格(元/台)
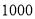
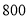
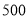
销售获利(元/台)
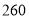
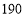
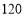
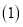 购买丙型设备 台(用含
购买丙型设备 台(用含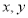 的代数式表示) ;
的代数式表示) ;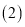 若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了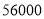 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?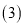 在第
在第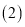 题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少? -
科目: 来源: 题型:
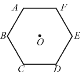
查看答案和解析>>【题目】如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O旋转多少度后能和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.

(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
相关试题

