【题目】【问题情境】
在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.

图① 图② 图③
证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)
【变式探究】
当点P在CB延长线上时,其余条件不变(如图3).试探索PD、PE、CF之间的数量关系并说明理由.
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;

【迁移拓展】
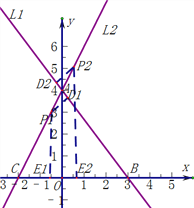
在直角坐标系中.直线l1:y=![]() 与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.

参考答案:
【答案】【变式探究】:详见解析;【结论运用】:4;【迁移拓展】:P1的坐标为(![]() ,3)或(
,3)或(![]() ,5)
,5)
【解析】试题分析:【变式探究】按照【问题情境】的证明思路即可解决问题.
【结论运用】过![]() 作
作![]() 利用问题情境中的结论可得
利用问题情境中的结论可得![]() ,易证
,易证![]() 只需求即可.
只需求即可.
【迁移拓展】分成两种情况进行讨论.
试题解析:【变式探究】:连接![]()
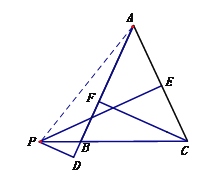
∵PD⊥AB,PE⊥AC,CF⊥AB,
![]()
![]()
![]()
![]()
【结论运用】过![]() 作
作![]() 垂足为
垂足为![]() ,如图④,
,如图④,
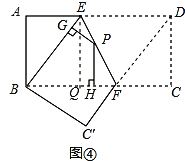
∵四边形![]() 是长方形,
是长方形, ![]()
![]()
由折叠可得: ![]()
![]()
![]()
![]()
![]()
∴四边形![]() 是长方形.
是长方形. ![]()
∵AD∥BC, ![]()
![]()
由问题情境中的结论可得: ![]()
![]() 的值为4.
的值为4.
【迁移拓展】
由题意得: ![]()
![]()
![]()
![]()
(1)由结论得: ![]()
![]()
即点![]() 的纵坐标为3,
的纵坐标为3,
又点![]() 在直线l2上 ∴
在直线l2上 ∴![]() =3 ,
=3 ,
∴![]() .
.
即点![]() 的坐标为
的坐标为![]()
(2) 由结论得: ![]()
![]() 即点
即点![]() 的纵坐标为5,
的纵坐标为5,
又点![]() 在直线l2上 ∴
在直线l2上 ∴![]() =5.
=5.
∴![]() .
.
即点![]() 的坐标为
的坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的余角的度数是 30°15′,那么这个角的补角的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年某市有23 000名初中毕业生参加了升学考试,为了解23 000名考生的升学成绩,从中抽取了200名考生的试卷进行统计分析,以下说法正确的是( )
A.23 000名考生是总体B.每名考生的成绩是个体
C.200名考生是总体的一个样本D.以上说法都不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:(x + 2)0 = 1,则( )
A.x = 3B.x = 1C.x为任意实数D.x ≠- 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(m-n)2=8,(m+n)2=4,则m2+n2=( )
A.32B.12C.6D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当方法解下列方程:
(1)(3x+1)2﹣9=0
(2)x2+4x﹣1=0
(3)3x2﹣2=4x
(4)(y+2)2=1+2y.
相关试题

