搜索
【题目】如果一个角的余角的度数是 30°15′，那么这个角的补角的度数是_____．
参考答案：
【答案】120°15′
【解析】
先根据余角的定义求出这个角的度数，再根据补角的定义求解即可．
解：∵一个角的余角的度数是30°15′，
∴这个角为90°-30°15′=59°45′，
∴这个角的补角的度数是180°-59°45′=120°15′．
故答案为：120°15′．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果 a+b+c＝0，且|a|＞|b|＞|c|．则下列式子中可能成立的是（ ）
A.c＞0，a＜0B.c＜0，b＞0
C.b＞0，c＜0D.b=0
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的解题过程：
用公式法解下列方程：
（1）2x2﹣3x﹣2=0．
解：a=___，b=___，c=___．
b2﹣4ac=___=___＞0．
=____=___，x1=__，x2=___．
（2）x（2x﹣
）=
x﹣3．解：整理，得___．
a=__，b=___，c=___．
b2﹣4ac=___=___．
=_____=____，x1=x2=__．
（3）（x﹣2）2=x﹣3．
解：整理，得______．
a=___，b=___，c=___．
b2﹣4ac=___=___＜0．
方程___实数根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程
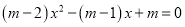.（其中m为实数）（1）若此方程的一个非零实数根为k，
① 当k = m时，求m的值；
② 若记
为y，求y与m的关系式；（2）当
＜m＜2时，判断此方程的实数根的个数并说明理由 -
科目： 来源： 题型：
查看答案和解析>>【题目】2018年某市有23 000名初中毕业生参加了升学考试，为了解23 000名考生的升学成绩，从中抽取了200名考生的试卷进行统计分析，以下说法正确的是（ ）
A.23 000名考生是总体B.每名考生的成绩是个体
C.200名考生是总体的一个样本D.以上说法都不正确
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：（x + 2）0 = 1，则（ ）
A.x = 3B.x = 1C.x为任意实数D.x ≠- 2
-
科目： 来源： 题型：
查看答案和解析>>【题目】【问题情境】
在△ABC中，AB=AC，点P为BC所在直线上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．当P在BC边上时（如图1），求证：PD+PE=CF．
图① 图② 图③
证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．（不要证明）
【变式探究】
当点P在CB延长线上时，其余条件不变（如图3）.试探索PD、PE、CF之间的数量关系并说明理由.
请运用上述解答中所积累的经验和方法完成下列两题：
【结论运用】
如图4，将长方形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；
【迁移拓展】
在直角坐标系中.直线l1：y=
与直线l2：y=2x+4相交于点A，直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
相关试题
