【题目】如图,在下面直角坐标系中,已知![]()

(1)求![]() 的面积
的面积
(2)若以点![]() 为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点
为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点![]() 的坐标
的坐标
(3)是否存在![]() 轴上的点
轴上的点![]() ,使
,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,若存在,求出点
倍,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)16;(2)(4,4)或(12,4)或(4,4);(3) 存在,点M的坐标为(24,0)或(8,0).
【解析】
(1)由A点坐标得到△ABO边OB上的高为|-4|,则可根据三角形面积公式计算△ABO的面积;
(2)用图形平移的特性:线段上的点坐标变化是一样的得出C点的坐标;
(3)M点在x轴上,那么![]() 和
和![]() 是登高的,只要找出底BM是OB的两倍的点M就行.
是登高的,只要找出底BM是OB的两倍的点M就行.
(1)![]() ;
;
(2) 以点![]() 为顶点画平行四边形,当把AB向右平移8个单位,即把点A(-4,-4)向右平移8个单位,得到C的坐标(4,4);当把OA向左平移8个单位,即把点A(-4,-4)向左平移8个单位得到C的坐标(-12,4);当把AB向上平移A移到O,xy轴坐标都增加了4,B的坐标也得增加4,得到C的坐标(-4,4),
为顶点画平行四边形,当把AB向右平移8个单位,即把点A(-4,-4)向右平移8个单位,得到C的坐标(4,4);当把OA向左平移8个单位,即把点A(-4,-4)向左平移8个单位得到C的坐标(-12,4);当把AB向上平移A移到O,xy轴坐标都增加了4,B的坐标也得增加4,得到C的坐标(-4,4),
∴C的坐标为(4,4)或(12,4)或(4,4);
(3)存在.
![]() ×|x+8|×4=2
×|x+8|×4=2![]() =32,解得x=8或24,
=32,解得x=8或24,
∴点M的坐标为(24,0)或(8,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,AB
 OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.(1)在t=3时,M点坐标 ,N点坐标 ;
(2)当t为何值时,四边形OAMN是矩形?
(3)运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】江汉路一服装店销售一种进价为50元/件的衬衣,生产厂家规定每件定价为60~150元.当定价为60元/件时,每星期可卖出70件,每件每涨价10元,一星期少卖出5件.
(1)当每件衬衣定价为多少元时(定价为10元的正整数倍),服装店每星期的利润最大?最大利润为多少元?
(2)请分析每件衬衣的定价在哪个范围内时,每星期的销售利润不低于2 700元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
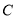 点是第二象限内一点,
点是第二象限内一点, 轴于
轴于 ,且
,且 是
是 轴正半轴上一点,
轴正半轴上一点, 是x轴负半
是x轴负半 轴上一点,且
轴上一点,且 .
.
(1)
 ( ),
( ), ( )
( )(2)如图2,设
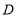 为线段
为线段 上一动点,当
上一动点,当 时,
时, 的角平分线与
的角平分线与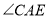 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点 ,求
,求 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为 )
) (3)如图3,当
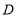 点在线段
点在线段 上运动时,作
上运动时,作 交
交 于
于 的平分线交于
的平分线交于 ,当
,当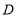 点在运动的过程中,
点在运动的过程中, 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=
 ,BE=2.
,BE=2.
求证:(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,在某个时刻停留在A处,规定以岗亭为原点,向北方向为正,这段时间行驶纪录如下(单位:千米)
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. (1)
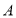 在岗亭哪个方向?距岗亭多远?
在岗亭哪个方向?距岗亭多远? (2)若摩托车行驶每千米耗油
 升,每升
升,每升 元,且最后返回岗亭,这一天耗油共需多少元?
元,且最后返回岗亭,这一天耗油共需多少元?
相关试题

