【题目】如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=![]() ,BE=2.
,BE=2.

求证:(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
参考答案:
【答案】证明:(1)连接OC,
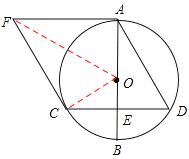
∵AF是⊙O切线,∴AF⊥AB。
∵CD⊥AB,∴AF∥CD。
∵CF∥AD,∴四边形FADC是平行四边形。
∵AB是⊙O的直径,CD⊥AB,
∴![]() 。
。
设OC=x,
∵BE=2,∴OE=x﹣2。
在Rt△OCE中,OC2=OE2+CE2,
∴![]() ,解得:x=4。
,解得:x=4。
∴OA=OC=4,OE=2。∴AE=6。
在Rt△AED中,![]() ,∴AD=CD。
,∴AD=CD。
∴平行四边形FADC是菱形。
(2)连接OF,
∵四边形FADC是菱形,∴FA=FC。
在△AFO和△CFO中,∵ ,∴△AFO≌△CFO(SSS)。
,∴△AFO≌△CFO(SSS)。
∴∠FCO=∠FAO=90°,即OC⊥FC。
∵点C在⊙O上,∴FC是⊙O的切线。
【解析】
试题分析:(1)连接OC,由垂径定理,可求得CE的长,又由勾股定理,可求得半径OC的长,然后由勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平行四边形,继而证得四边形FADC是菱形;
(2)连接OF,易证得△AFO≌△CFO,继而可证得FC是⊙O的切线。
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下面直角坐标系中,已知


(1)求
 的面积
的面积(2)若以点
 为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点
为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点 的坐标
的坐标 (3)是否存在
 轴上的点
轴上的点 ,使
,使 的面积是
的面积是 的面积的
的面积的 倍,若存在,求出点
倍,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 点是第二象限内一点,
点是第二象限内一点, 轴于
轴于 ,且
,且 是
是 轴正半轴上一点,
轴正半轴上一点, 是x轴负半
是x轴负半 轴上一点,且
轴上一点,且 .
.
(1)
 ( ),
( ), ( )
( )(2)如图2,设
 为线段
为线段 上一动点,当
上一动点,当 时,
时, 的角平分线与
的角平分线与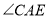 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点 ,求
,求 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为 )
) (3)如图3,当
 点在线段
点在线段 上运动时,作
上运动时,作 交
交 于
于 的平分线交于
的平分线交于 ,当
,当 点在运动的过程中,
点在运动的过程中, 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,在某个时刻停留在A处,规定以岗亭为原点,向北方向为正,这段时间行驶纪录如下(单位:千米)
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. (1)
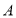 在岗亭哪个方向?距岗亭多远?
在岗亭哪个方向?距岗亭多远? (2)若摩托车行驶每千米耗油
 升,每升
升,每升 元,且最后返回岗亭,这一天耗油共需多少元?
元,且最后返回岗亭,这一天耗油共需多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠EDF的度数为( )

A.34°B.56°C.62°D.28°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点
 表示的数为
表示的数为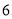 ,点
,点 表示的数为
表示的数为 ,点
,点 到点
到点 、点
、点 的距离相等,动点
的距离相等,动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为 (
( 大于
大于 秒.
秒.
(1)点
 表示的数是______.
表示的数是______.(2)求当
 等于多少秒时,点
等于多少秒时,点 到达点
到达点 处?
处?(3)点
 表示的数是______(用含字母
表示的数是______(用含字母 的式子表示)
的式子表示)(4)求当
 等于多少秒时,
等于多少秒时, 、
、 之间的距离为
之间的距离为 个单位长度.
个单位长度.
相关试题

