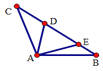
【题目】如图△ABC中,AB=AC,∠BAC=120°,∠DAE=60°,BE=4,CD=6,则DE的长为________.
参考答案:
【答案】![]()
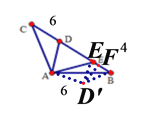
【解析】分析:把△ADC绕点A顺时针旋转120°得到△AD′B,再结合条件可证明△AD′E≌△ADE,可得ED′=ED,过D′作DF⊥BE于点F,可求得EF和D′F的长,在Rt△D′FE中可求得ED′,
则可求得ED.
详解:∵AB=AC,
∴可把△ADC绕点A顺时针旋转120°得到△AD′B,
∴BD′=DC=6,AD′=AD,∠D′AB=∠DAC,
∵∠BAC=120°,∠EAD=60°,
∴∠BAE+∠DAC=60°,
∴∠D′AE=∠D′AB+∠BAE=60°,
在△D′AE和△DAE中
AD'=AD,
∠D'AE=∠DAE,
AE=AE,
∴△D′AE≌△DAE(SAS),
∴D′E=DE,
过D′作DF⊥BE于点F,连接D′F,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠C=∠D′BA=30°,
∴∠D′BF=60°,
∴∠BD′F=30°,
∴BF=![]() BD′=3,D′F=3
BD′=3,D′F=3![]() ,
,
∵BE=4,
∴FE=BE-BF=1,
在Rt△D′FE中,由勾股定理可得D′E=![]() ,
,
∴ED=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三边为a、b、c,由下列条件不能判断它是直角三角形的是( )
A. ∠A: ∠B: ∠C =3∶4∶5 B. ∠A=∠B+∠C
C. a2=(b+c)(b-c) D. a:b:c =1∶2∶
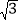
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A
1
2
3
4
5
B
0
3
8
15
24
A. 99 B. 100 C. 101 D. 102
-
科目: 来源: 题型:
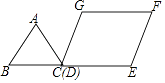
查看答案和解析>>【题目】如图,等边△ABC边长为2,四边形DEFG是平行四边形,DG=2,DE=3,∠GDE=60°,BC和DE在同一条直线上,且点C与点D重合,现将△ABC沿D→E的方向以每秒1个单位的速度匀速运动,当点B与点E重合时停止,则在这个运动过程中,△ABC与四边形DEFG的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A.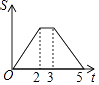
B.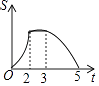
C.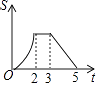
D.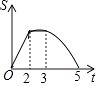
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣20+8﹣(﹣1)+(﹣4)
(2)
 ×(﹣
×(﹣ )2÷(﹣0.5)3
)2÷(﹣0.5)3(3)4﹣6÷(﹣2)×(﹣
 )
)(4)(﹣36)×(﹣
 +
+ ﹣
﹣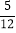 )
)(5)(﹣2)2×0.5﹣(﹣1.6)2÷(﹣2)3
(6)﹣14÷(﹣4)﹣(﹣
 )2×(﹣3)+|(﹣1)2﹣2|
)2×(﹣3)+|(﹣1)2﹣2| -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形ABC中,AB=AC=10,BC=12,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1
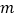 ).
).
相关试题

