【题目】在等腰三角形ABC中,AB=AC=10,BC=12,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=______.
参考答案:
【答案】9.6
【解析】分析:如图连接AD,作AH⊥BC于H.首先利用勾股定理求出AH,再根据S△ABC=S△ABD+S△ACD,DE⊥AB,DF⊥AC,可得![]() BCAH=
BCAH=![]() ABDE+
ABDE+![]() ACDF,由此即可解决问题.
ACDF,由此即可解决问题.
详解:如图,连接AD,作AH⊥BC于H.
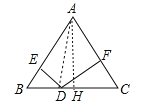
∵AB=AC=10,AH⊥BC,∴BH=CH=6.在Rt△ABH中,AH=![]() =
=![]() =8.
=8.
∵S△ABC=S△ABD+S△ACD,DE⊥AB,DF⊥AC,∴![]() BCAH=
BCAH=![]() ABDE+
ABDE+![]() ACDF,∴6×8=5DE+5DF,∴DE+DF=9.6.
ACDF,∴6×8=5DE+5DF,∴DE+DF=9.6.
故答案为:9.6.
-
科目: 来源: 题型:
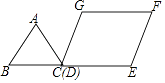
查看答案和解析>>【题目】如图,等边△ABC边长为2,四边形DEFG是平行四边形,DG=2,DE=3,∠GDE=60°,BC和DE在同一条直线上,且点C与点D重合,现将△ABC沿D→E的方向以每秒1个单位的速度匀速运动,当点B与点E重合时停止,则在这个运动过程中,△ABC与四边形DEFG的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A.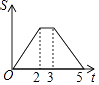
B.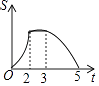
C.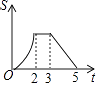
D.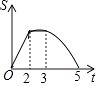
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,AB=AC,∠BAC=120°,∠DAE=60°,BE=4,CD=6,则DE的长为________.
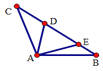
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣20+8﹣(﹣1)+(﹣4)
(2)
 ×(﹣
×(﹣ )2÷(﹣0.5)3
)2÷(﹣0.5)3(3)4﹣6÷(﹣2)×(﹣
 )
)(4)(﹣36)×(﹣
 +
+ ﹣
﹣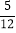 )
)(5)(﹣2)2×0.5﹣(﹣1.6)2÷(﹣2)3
(6)﹣14÷(﹣4)﹣(﹣
 )2×(﹣3)+|(﹣1)2﹣2|
)2×(﹣3)+|(﹣1)2﹣2| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1
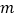 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过⊙O外一点P向⊙O作两条切线,切点分别为A,B,若⊙O半径为2,∠APB=60°,则图中阴影部分的面积为 .

-
科目: 来源: 题型:
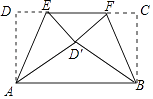
查看答案和解析>>【题目】如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为 .
相关试题

