【题目】【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示: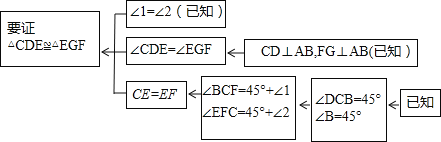
根据上述思路,请你完整地书写这道练习题的证明过程;
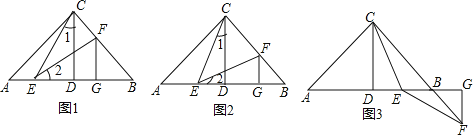
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、AE=![]() BF.
BF.
【解析】
试题分析:(1)、先证明CE=EF,根据AAS即可证明△CDE≌△EGF;(2)、先证∠ACE=∠2,再证明△ACE≌△BEF,即可得出AE=BF;(3)、作EH⊥BC与H,设DE=x,求出AE=3x,再证出BF=![]() x,即可得出结论.
x,即可得出结论.
试题解析:(1)、∵AC=BC,∠ACB=90°, ∴∠A=∠B=45°, ∵CD⊥AB, ∴∠CDB=90°,
∴∠DCB=45°, ∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2, ∴∠ECF=∠EFC,
∴CE=EF, ∵CD⊥AB,FG⊥AB, ∴∠CDE=∠EGF=90°,
在△CDE和△EGF中,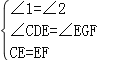 ,∴△CDE≌△EGF(AAS);
,∴△CDE≌△EGF(AAS);
(2)、由(1)得:CE=EF,∠A=∠B, ∵CE平分∠ACD, ∴∠ACE=∠1, ∵∠1=∠2,∴∠ACE=∠2,
在△ACE和△BEF中, ,∴△ACE≌△BEF(AAS),∴AE=BF;
,∴△ACE≌△BEF(AAS),∴AE=BF;
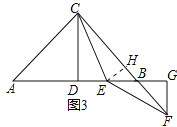
(3)、AE=![]() BF,作EH⊥BC与H,如图3所示:
BF,作EH⊥BC与H,如图3所示:
设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x, 根据勾股定理得:BC=AC=2![]() x,
x,
∵∠ABC=45°,EH⊥BC, ∴BH=![]() x, ∴CH=BC﹣BH=
x, ∴CH=BC﹣BH=![]() x, ∵EC=EF, ∴FH=CH=
x, ∵EC=EF, ∴FH=CH=![]() x,
x,
∴BF=![]() x﹣
x﹣![]() x=
x=![]() x, ∴
x, ∴![]() , ∴AE=
, ∴AE=![]() BF.
BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班12位同学参加每周一次的教室卫生大扫除,有扫地、擦玻璃和擦课桌椅三个项目,扫地的面积为88 m2,擦玻璃的面积为32 m2,根据实际情况将三个项目的面积分配情况和每人每分钟完成各项目的工作量制作如下统计图:
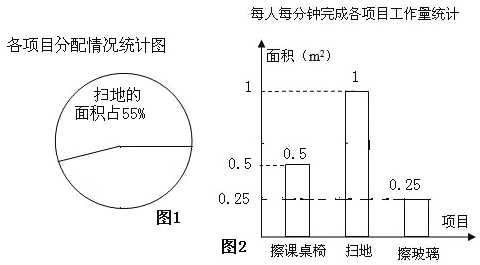
(1)擦课桌椅的面积为__________,请补全图1中的各项目面积分配情况扇形统计图;
(2)卫生委员设计两种方案:
方案一:12位同学先一起完成扫地任务,再一起完成擦玻璃任务,最后一起完成擦课桌椅任务;
方案二:12位同学先一起完成扫地任务后,再把这12位同学分成两组,每组6人,一组擦玻璃,一组去擦课桌椅.
你认为这哪种方案完成大扫除任务所用的时间少,少多少时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(2019,﹣2018)关于x轴对称的点的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
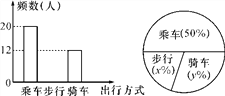
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )
A.点P在圆上
B.点P在圆内
C.点P在圆外
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】一扇窗户打开后,用窗钩就可将窗户固定,其几何原理是_______.
-
科目: 来源: 题型:
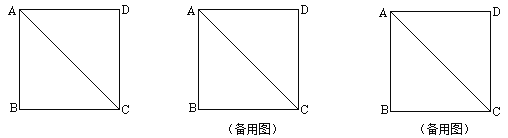
查看答案和解析>>【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.
探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.
相关试题

