【题目】已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )
A.点P在圆上
B.点P在圆内
C.点P在圆外
D.不能确定
参考答案:
【答案】B
【解析】解:∵OP=3<4,故点P与⊙O的位置关系是点在圆内.
故选B.
点在圆上,则d=r;点在圆外,d>r;点在圆内,d<r(d即点到圆心的距离,r即圆的半径).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(2019,﹣2018)关于x轴对称的点的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
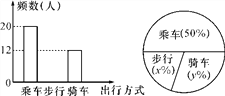
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
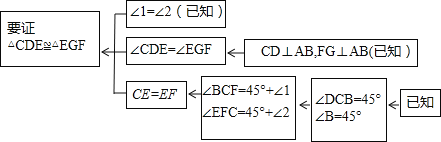
根据上述思路,请你完整地书写这道练习题的证明过程;
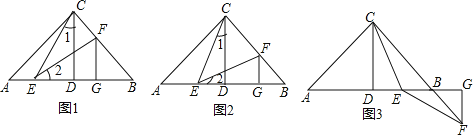
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一扇窗户打开后,用窗钩就可将窗户固定,其几何原理是_______.
-
科目: 来源: 题型:
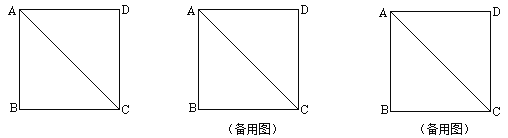
查看答案和解析>>【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.
探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣1)2+3的顶点坐标为( )
A.(2,1)
B.(2,﹣1)
C.(﹣1,3)
D.(1,3)
相关试题

