【题目】某学校一班级开展为贫困山区学生捐钱助学活动,该班有20名学生捐出了自己的零花钱,捐款数如下:(单位:元)
19 | 20 | 25 | 30 | 28 | 27 | 26 | 21 | 20 | 22 | 24 | 23 | 25 | 29 | 27 | 28 | 27 | 30 | 19 | 20 |
该班老师准备将此次活动的捐款数据制成频数分布直方图,在制图时请你帮老师算出以下数据:
(1)计算最大值与最小值的差;
(2)若选定组距为2计算将这20个数据分成的组数;并计算将第一组的起点定为18.5时捐款数在26.5-28.5范围内的频数;
(3)计算第一组和最后一组这两个组内包含的所有样本的平均数
参考答案:
【答案】(1)最大值与最小值的差:11;(2)若取选定组距为2,则此20个数据将分为6组,频数为5;(3)平均数为:![]() .
.
【解析】
(1)找出最大值和最小值,然后相减即可;
(2)用最大值与最小值的差除以2,即可得到组数,注意结果用首尾法;
(3)先找出第一组和最后一组中的数,根据平均数的计算方法求解即可.
解:(1)这50个数据中,最大值是30,最小值是19
![]()
(2)![]()
∴若取选定组距为2,则此20个数据将分为6组
由于在26.5-28.5范围内的数有28,27,27,28,27共5个数,所以频数为5
(3)第一组内含的样本有:19,19,20,20,20
最后一组内包含的样本有:29,30,30
所以其平均数为:![]()
注:学生用组中值计算平均数即;
![]() 也可得分。
也可得分。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=_____°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中, D,E,F三点分别在AB,AC,BC上,过点D的直线与线段EF的交点为点M,已知2∠1-∠2=150°,2∠ 2-∠1=30°.
(1)求证:DM∥AC;
(2)若DE∥BC,∠C =50°,求∠3的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算、求解:
(1)用代人消元法解方程组:
 ;
;(2)加减消元法解方程组:
 ;
;(3)计算:
 ;
;(4)解不等式组
 ,并把解集在数轴上表示出来,
,并把解集在数轴上表示出来,
-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设资源节约型、环境友好型社会,切实做好节能减排工作,某市决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度/时,实行“基本电价”;当居民家庭月用电量超过80千瓦时,超过部分实行“提高电价”已知小张家2017年2月份用电100千瓦时,上缴电费68元;3月份用电120千瓦时,上缴电费88元若7月份小张家预计用电130千瓦时,请预算小张家7月份应上缴的电费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点
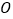 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到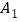 (0,1),
(0,1),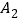 (1,1),
(1,1), (1,0),
(1,0),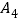 (2,0),…那么点
(2,0),…那么点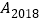 的坐标为__________.
的坐标为__________.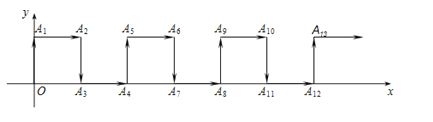
相关试题

