【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

参考答案:
【答案】(1)证明见解析;
(2)a,b,c三者存在的关系是a+b>c,理由见解析.
【解析】(1)首先根据题意得B′F=BF,∠B′FE=∠BFE,接着根据平行线的性质和等腰三角形的判定即可证明B′E=BF;
(2)解答此类题目时要仔细读题,根据三角形三边关系求解分类讨论解答,要提高全等三角形的判定结合勾股定理解答.
证明:(1)由题意得B′F=BF,∠B′FE=∠BFE,
在矩形ABCD中,AD∥BC,
∴∠B′EF=∠BFE,
∴∠B′FE=∠B'EF,
∴B′F=BE,
∴B′E=BF;
解:(2)答:a,b,c三者关系不唯一,有两种可能情况:
(ⅰ)a,b,c三者存在的关系是a2+b2=c2.
证明:连接BE,则BE=B′E,
由(1)知B′E=BF=c,
∴BE=c.
在△ABE中,∠A=90°,
∴AE2+AB2=BE2,
∵AE=a,AB=b,
∴a2+b2=c2;
(ⅱ)a,b,c三者存在的关系是a+b>c.
证明:连接BE,则BE=B′E.
由(1)知B′E=BF=c,
∴BE=c,
在△ABE中,AE+AB>BE,
∴a+b>c.
“点睛”此题以证明和探究结论形式来考查矩形的翻折、等角对等边、三角形全等、勾股定理等知识.第一,较好考查学生表述数学推理和论证能力,第(1)问重点考查了学生逻辑推理的能力,主要利用等角对等边、翻折等知识来证明;第二,试题呈现显示了浓郁的探索过程,试题设计的起点低,图形也很直观,也可通过自已动手操作,寻找几何元素之间的对应关系,形成较为常规的方法解决问题,第(2)问既考查了学生对勾股定理掌握的程度又考查学生的数学猜想和探索能力,这对于培养学生创新意识和创新精神十分有益;第三,解题策略多样化在本题中得到了充分的体现.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x<0,y>0,x+y<0,那么下列关系式中正确的是( )
A.x>y>﹣y>﹣x
B.﹣x>y>﹣y>x
C.y>﹣x>﹣y>x
D.﹣x>y>x>﹣y -
科目: 来源: 题型:
查看答案和解析>>【题目】小莉的爸爸买了某演唱会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果;
(2)哥哥设计的游戏规则公平吗?为什么?若不公平,请设计一种公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的主视图、左视图、俯视图都是圆形,这个几何体可能是( )
A.圆柱B.圆锥C.球D.半球
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上
②把弯曲的公路改直,就能够缩短路程
③从A地到B地架设电线,总是尽可能沿着线段AB来架设
其中,可以用“两点之间,线段最短”来解释的现象是______(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣1=(﹣1)0,则a=__.
-
科目: 来源: 题型:
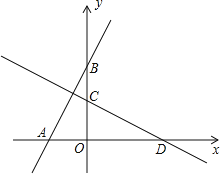
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,过点A(﹣2,0)的直线交y轴正半轴于点B(0,4),将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.且点C(0,3).
(1)求直线AB的函数关系式;
(2)连接BD,求△ABD的面积.
相关试题

