【题目】如图,![]() 的四个内角的平分线分别相交于点
的四个内角的平分线分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() ,四边形
,四边形![]() 是怎样的特殊四边形?证明你的结论.
是怎样的特殊四边形?证明你的结论.

参考答案:
【答案】矩形,证明见解析
【解析】
由于四边形ABCD是平行四边形,那么AB∥CD,利用平行线的性质可得∠ABC+∠BCD=180°,而BH,CH分别平分∠ABC与∠BCD,则∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,那么有∠HBC+∠HCB=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠F=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.
∠BCD,那么有∠HBC+∠HCB=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠F=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.
四边形EFGH是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,
∠BCD,
∴∠HBC+∠HCB=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.
-
科目: 来源: 题型:
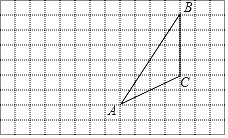
查看答案和解析>>【题目】画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.
(1)将△ABC向左平移4格,再向下平移1格,请在图中画出平移后的△A'B'C';
(2)利用网格线在图中画出△ABC的中线CD,高线AE;
(3)△A'B'C'的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD;
(2)若FG⊥BC于点H,BC平分∠ABD,∠D=112°,求∠1的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.

(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2
 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )
A. ﹣
﹣ 
B. ﹣
﹣ 
C. ﹣
﹣ 
D. +
+ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
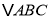 的位置如图所示.
的位置如图所示.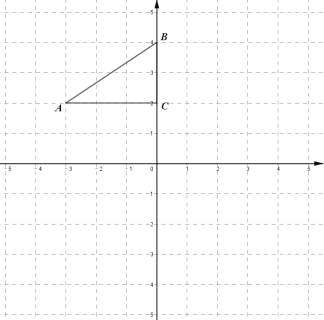
(1)画出
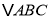 先向右平移3个单位,再向下平移6个单位后得到的
先向右平移3个单位,再向下平移6个单位后得到的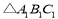 ,并写出
,并写出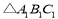 ,各顶点的坐标;
,各顶点的坐标;(2)画出
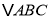 绕点
绕点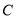 逆时针旋转
逆时针旋转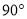 后得到的
后得到的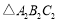 ,并写出
,并写出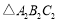 ,各顶点的坐标.
,各顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.

相关试题

