【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 . 
参考答案:
【答案】15°
【解析】解:∵∠BAC=90°,∠B=60°,
∴∠ACB=90°﹣60°=30°,
∵△AB′C由△ABC绕点A顺时针旋转90°得到,
∴AC′=AC,∠C′AB′=∠CAB=90°,∠AC′B′=30°,
∴△ACC′为等腰直角三角形,
∴∠AC′C=45°,
∴∠CC′B′=∠AC′C﹣∠AC′B′=45°﹣30°=15°.
所以答案是15°.
【考点精析】关于本题考查的旋转的性质,需要了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并回答问题. 事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:

(1)一个直角三角形的两条直角边分别为6、8,那么这个直角三角形斜边长为 .
(2)如图1,AD⊥BC 于D,AD=BD,AC=BE,AC=3,DC=1,求BD的长度.
(3)如图2,点A在数轴上表示的数是 ,请用类似的方法在图2数轴上画出表示数
 的B点(保留作图痕迹).
的B点(保留作图痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=
 AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.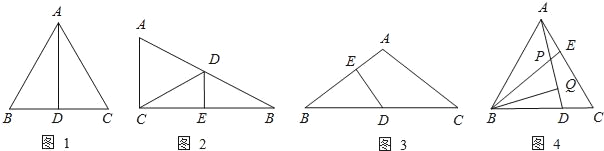
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长= .
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA= .
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b相交.
(1)已知∠1=40°,求∠2,∠3,∠4;
(2)已知∠2+∠4=280°,求各角;
(3)已知∠1∶∠2=2∶7,求各角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品店购进一批单件为40元的球服,如果按单价60元销售样,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单件为多少元时,月销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在学校开展的小制作评比活动中,二年级六个班都参加了比赛,根据他们上交作品的件数,绘制直方图如右.已知从左至右各长方形高的比为2∶3∶4∶2∶3∶1,小制作件数最多的三班上交了16件.经评选各班获奖件数如下表:

在这次评选中,获奖率最高的两个班级依次是( ).
A. 5班、3班 B. 3班、4班 C. 5班、6班 D. 6班、5班
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB与CD交于点O,OM为射线.
(1)写出∠BOD的对顶角;
(2)写出∠BOD与∠COM的邻补角;
(3)已知∠AOC=70°,∠BOM=80°,求∠DOM和∠AOM的度数.

相关试题

