【题目】阅读下列材料,并回答问题. 事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:

(1)一个直角三角形的两条直角边分别为6、8,那么这个直角三角形斜边长为 .
(2)如图1,AD⊥BC 于D,AD=BD,AC=BE,AC=3,DC=1,求BD的长度.
(3)如图2,点A在数轴上表示的数是 ,请用类似的方法在图2数轴上画出表示数![]() 的B点(保留作图痕迹).
的B点(保留作图痕迹).
参考答案:
【答案】(1)10;(2)BD= 2![]() ;(3)﹣
;(3)﹣![]() .
.
【解析】整体分析:
(1)用勾股定理求斜边的长;(2)在Rt△ADC中用勾股定理求AD的长,由BD=AD求解;(3)用勾股定理解题.
解:(1)直角三角形的两条直角边分别为6、8,
则这个直角三角形斜边长=![]() =10,
=10,
故答案为:10;
(2)在Rt△ADC中,AD=![]() =2
=2![]() ,
,
∴BD=AD=2![]() ;
;
(3)点A在数轴上表示的数是:﹣![]() =﹣
=﹣![]() ,
,
由勾股定理得,OC=![]() ,
,
以O为圆心、OC为半径作弧交x轴于B,则点B即为所求,
故答案为﹣![]() .
.

-
科目: 来源: 题型:
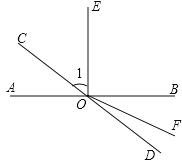
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )

A. 95° B. 65°
C. 50° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB和CD相交于O点,OE⊥AB,∠1=55°,则∠BOD= 度;若OF平分∠DOB,则∠EOF的度数是 度.
-
科目: 来源: 题型:
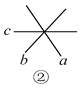
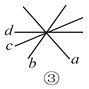
查看答案和解析>>【题目】观察下列图形,寻找对顶角(不含平角).
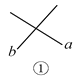
(1)如图①,图中共有____对对顶角;
(2)如图②,图中共有____对对顶角;
(3)如图③,图中共有____对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角对数的关系,猜想:若有n条直线相交于一点,则共可形成__________对对顶角;
(5)若有180条直线相交于一点,则可形成________对对顶角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=
 AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.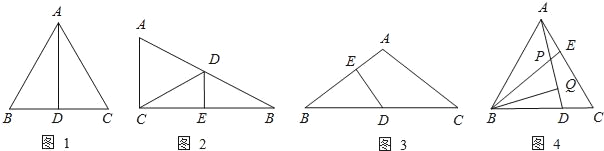
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长= .
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA= .
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b相交.
(1)已知∠1=40°,求∠2,∠3,∠4;
(2)已知∠2+∠4=280°,求各角;
(3)已知∠1∶∠2=2∶7,求各角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 .

相关试题

