【题目】如图所示,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠DEC=60°,CE=2DE=4cm,求CD的长.

参考答案:
【答案】(1)见解析;(2)CD=2![]()
【解析】整体分析:
(1)用SAS证明△BAE≌△DAE,判断四边形ABED的四边都相等;(2)过点D作DF∥AE交BC于点F,判断四边形AEFD是平行四边形,△DEF是等边三角形,证明△EDC是直角三角形,用勾股定理求解.
(1)证明:如图,∵AE平分∠BAD,∴∠1=∠2,
∵AB=AD,AE=AE,
∴△BAE≌△DAE,
∴BE=DE,
∵AD∥BC,∴∠2=∠3=∠1,∴AB=BE,
∴AB=BE=DE=AD,
∴四边形ABED是菱形.
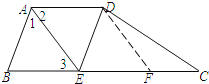
(2)解:如图,过点D作DF∥AE交BC于点F,则四边形AEFD是平行四边形,
∴DF=AE,AD=EF,
∵四边形ABED是菱形,
∴AB=BE=DE=AD,
∴DE=EF,
又∵∠ABC=60°,
∴∠DEF=60°,
∴△DEF是等边三角形,
∵CE=2DE,∴EF=FC,
∴DF=EF=FC,
∴△CDE是直角三角形.
由勾股定理求得CD=2![]() .
.
-
科目: 来源: 题型:
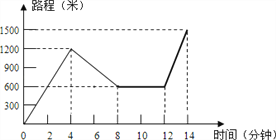
查看答案和解析>>【题目】小红星期天从家里出发汽车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到学校的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快速度是多少米/分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )
A.(9﹣7)x=1
B.(9+7)x=1
C.( +
+  )x=1
)x=1
D.( ﹣
﹣  )x=1
)x=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数
 ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点
 ,第2次接着运动到点
,第2次接着运动到点 ,第3次接着运动到点
,第3次接着运动到点 ,
, 按这样的运动规律,经过第2017次运动后,动点P的坐标是______,经过第2018次运动后,动点P的坐标是______.
按这样的运动规律,经过第2017次运动后,动点P的坐标是______,经过第2018次运动后,动点P的坐标是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.
相关试题

