【题目】已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC. 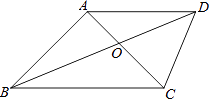
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
参考答案:
【答案】
(1)解:证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠DAC=∠ABC,
∴∠DAC=∠ACB.
∴AD∥BC,
∴∠ADB=∠CBD.
又∵AB=AD,
∴∠ADB=∠ABD.
∴∠ABD=∠CBD.
∴BD平分∠ABC;
(2)解:解:过点O作OE⊥BC于E,
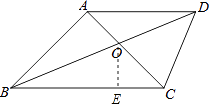
∵∠DAC=45°,∠DAC=∠ABC,
∴∠ABC=∠ACB=45°,
∴∠B AC=90°,
∵BD平分∠ABC,
∴OE=OA=1.
在Rt△OEC中,∠ACB=45°,OE=1,
∴OC= ![]() .
.
【解析】(1)根据等腰三角形的性质、平行线的性质以及角平分线的定义证明;(2)过点O作OE⊥BC于E,根据角平分线的性质得到OE=OA,根据勾股定理计算即可.
-
科目: 来源: 题型:
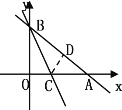
查看答案和解析>>【题目】如图,一次函数的图像与x轴、y轴分别交于A、B两点,且A、B的坐标分别为(4,0),(0,3).
(1)求一次函数的表达式.
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D处,
求直线BC的表达式.
-
科目: 来源: 题型:
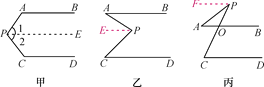
查看答案和解析>>【题目】阅读下列解答过程:(1)如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
(2)如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥DF,∠D+∠B=180°,

(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(1,2),直线l2与x轴交于点B(3,0).

(1)分别求直线l1和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D左方时,写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )
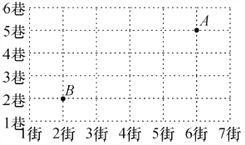
A. (2,2)→(2,5)→(5,6) B. (2,2)→(2,5)→(6,5)
C. (2,2)→(6,2)→(6,5) D. (2,2)→(2,3)→(6,3)→(6,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:
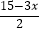 ≥7﹣x,并把它的解集在数轴上表示出来.
≥7﹣x,并把它的解集在数轴上表示出来. 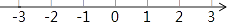
相关试题

