【题目】如图,时钟是我们常见的生活必需品,其中蕴含着许多数学知识.

(1)我们知道,分针和时针转动一周都是 度,分针转动一周是 分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动 度,时针每分钟转动 度.
(2)从5:00到5:30,分针与时针各转动了多少度?
(3)请你用方程知识解释:从1:00开始,在1:00到2:00之间,是否存在某个时刻,时针与分针在同一条直线上?若不存在,说明理由;若存在,求出从1:00开始经过多长时间,时针与分针在同一条直线上.
参考答案:
【答案】(1)360,60,6,0.5.(2)15°;(3)经过![]() 分钟或
分钟或![]() 分钟时针与分针在同一条直线上.
分钟时针与分针在同一条直线上.
【解析】试题分析:(1)利用钟表盘的特征解答.表盘一共被分成60个小格,每一个小格所对角的度数是6°;
(2)从5:00到5:30,分针转动了30个格,时针转动了2.5个格,即可求解;
(3)时针与分针在同一条直线上,分两种情况:①分针与时针重合;②分针与时针成180°,
设出未知数,,列出方程求解即可.
试题解析:(1)分针和时针转动一周都是360度,分针转动一周是60分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动360°÷60=6度,时针每分钟转动360°÷720=0.5度.
故答案为:360,60,6,0.5.
(2)从5:00到5:30,分针转动了:6°×30=180°,时针转动了6°×2.5=15°;
(3)从1:00开始,在1:00到2:00之间,存在某个时刻,时针与分针在同一条直线上.
设x分钟分针与时针重合,
则,0.5+30°=6x
解得 ![]()
设y分钟分针与时针成180°,
0.5y+30°+180°=6y
解得 ![]()
∴经过![]() 分钟或
分钟或![]() 分钟时针与分针在同一条直线上.
分钟时针与分针在同一条直线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为
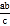
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
(1)求线段MN的长.
(2)当C在AB延长线上时,其他条件不变,求线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点F是对角线BD上的一点,EF∥AB交AD于点E,FG∥BC交DC于点G,四边形EFGP是平行四边形,给出如下结论:
①四边形EFGP是菱形;
②△PED为等腰三角形;
③若∠ABD=90°,则△EFP≌△GPD;
④若四边形FPDG也是平行四边形,则BC∥AD且∠CDA=60°.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在数轴上A,B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF=_______;
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,α=_______
②猜想∠BCE和α的数量关系,并证明;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α-β|=40°,请直接写出t的值为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一条直线过点(0,4),且与抛物线y=
 x2交于A,B两点,其中点A的横坐标是﹣2.
x2交于A,B两点,其中点A的横坐标是﹣2.
(1)求这条直线的函数关系式及点B的坐标.
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
相关试题

