【题目】如图,已知A(-4,n),B(1,-4)是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.

(1)求反比例函数和一次函数的解析式;
(2)求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标及△
的坐标及△![]() 的面积;
的面积;
(3)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
参考答案:
【答案】(1)反比例函数![]() ,一次函数
,一次函数![]() (2)C(-3,0);
(2)C(-3,0);![]()
(3)﹣4<![]() <0和
<0和![]() >1
>1
【解析】
试题分析:(1)∵反比例函数![]() 过点B(1,-4)
过点B(1,-4)
∴![]() ∴
∴![]()
当![]() ∴A(-4,1)
∴A(-4,1)
∴![]() ∴
∴![]()
∴ ![]()
(2)在直线![]() 中,当
中,当![]() 时,
时,![]() ,∴C(-3,0)
,∴C(-3,0)
同理可求直线![]() 与
与![]() 轴交点的坐标为(0,-3)
轴交点的坐标为(0,-3)
∴![]() =
=![]()
(3)由函数图象得不等式![]() 的解集即是
的解集即是![]() 不等式的解,从图象上来看就是反比例函数图象高于一次函数图象的部分所对应的x的取值范围,所以不等式
不等式的解,从图象上来看就是反比例函数图象高于一次函数图象的部分所对应的x的取值范围,所以不等式![]() 的解集是﹣4<
的解集是﹣4<![]() <0和
<0和![]() >1
>1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境1:如图1,AB∥CD,P是ABCD内部一点,P在BD的右侧,探究∠B,∠P,∠D之间的关系?
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)

问题情境2
如图3,AB∥CD,P是AB,CD内部一点,P在BD的左侧,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)
问题迁移:请合理的利用上面的结论解决以下问题:
已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F
(1)如图4,若∠E=80°,求∠BFD的度数;
(2)如图5中,∠ABM=
 ∠ABF,∠CDM=
∠ABF,∠CDM= ∠CDF,写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,写出∠M与∠E之间的数量关系并证明你的结论.(3)若∠ABM=
 ∠ABF,∠CDM=
∠ABF,∠CDM= ∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M= .
∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB//DC,AB=DC,且AB=6cm,BC=8cm,对角线AC =10cm,
(1)求证:四边形ABCD是矩形;
(2)如图(2),若动点Q从点C出发,在CA边上以每秒5cm的速度向点A匀速运动,同时动点P从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,运动时间为t秒(0≤t<2),连接BQ、AP,若AP⊥BQ,求t的值;
(3)如图(3),若点Q在对角线AC上,CQ=4cm,动点P从B点出发,以每秒1cm的速度沿BC运动至点C止.设点P运动了t秒,请你探索:从运动开始,经过多少时间,以点Q、P、C为顶点的三角形是等腰三角形?请求出所有可能的结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形
 中,
中, 为边
为边 的中点,
的中点, 与对角线
与对角线 交于点
交于点 ,过
,过 作
作 于点
于点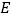 ,
, .
.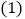 若
若 ,求
,求 的长;
的长; 求证:
求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
相关试题

