【题目】如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P , 垂足为E , 连接CP , 求∠CPB的度数.
参考答案:
【答案】解答:解:如下图,先连接AP , 由四边形ABCD是菱形,∠ADC=72°,可得∠BAD=180°-72°=108°,根据菱形对角线的对称性可得∠ABD=∠ADB= ![]() ∠ADC=
∠ADC= ![]() ,EP是AD的垂直平分线,由垂直平分线的对称性可得∠DAP=∠ADB=36°,∴∠PAB=∠DAB-∠DAP=108°-36°=72°,在△BAP中,∠APB=180°-∠BAP-∠ABP=180°-72°-36°=72°,由菱形对角线的对称性可得∠CPB=∠APB=72°.
,EP是AD的垂直平分线,由垂直平分线的对称性可得∠DAP=∠ADB=36°,∴∠PAB=∠DAB-∠DAP=108°-36°=72°,在△BAP中,∠APB=180°-∠BAP-∠ABP=180°-72°-36°=72°,由菱形对角线的对称性可得∠CPB=∠APB=72°.
【解析】本题开放性较强,解法有多种,可以从菱形、线段垂直平分线的性质、对称等方面去寻求解答方法,在这些方法中,最容易理解和表达的应为对称法,这也应该是本题考查的目的;灵活应用菱形、垂直平分线的对称性,可使解题过程更为简便快捷.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥y轴,A点的坐标为(﹣1,2),并且AB=4,则B的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接一个四边形的各边中点,得到一个矩形,则下列四边形中:①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.满足条件的四边形是______(把你认为正确的序号填在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某果园2014年猕猴桃产量为100吨,2016年猕猴桃产量为150吨,设该果园猕猴桃产量的年平均增长率为x,则根据题意可列方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)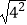 = ,
= , 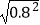 = ,
= , 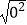 = ,
= , 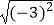 = ,
= , 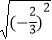 = ,
= ,
(2)根据计算结果,回答: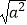 一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.
一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.
(3)利用你总结的规律,计算: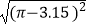 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F , 点E为垂足,连接DF , 求∠CDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.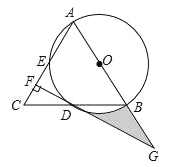
相关试题

