【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F , 点E为垂足,连接DF , 求∠CDF的度数.
参考答案:
【答案】解答:解:如图,连接BF , 在△BCF和△DCF中,∵CD=CB , ∠DCF=∠BCF , CF=CF , ∴△BCF≌△DCF , ∴∠CBF=∠CDF , ∵FE垂直平分AB , ∠BAF= ![]() ×80°=40°∴∠ABF=∠BAF=40°,∵∠ABC=180°-80°=100°,∠CBF=100°-40°=60°,∴∠CDF=60°.
×80°=40°∴∠ABF=∠BAF=40°,∵∠ABC=180°-80°=100°,∠CBF=100°-40°=60°,∴∠CDF=60°.
【解析】连接BF , 利用SAS判定△BCF≌△DCF , 从而得到∠CBF=∠CDF , 根据已知可注得∠CBF的度数,则∠CDF也就求得了.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某果园2014年猕猴桃产量为100吨,2016年猕猴桃产量为150吨,设该果园猕猴桃产量的年平均增长率为x,则根据题意可列方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P , 垂足为E , 连接CP , 求∠CPB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)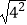 = ,
= , 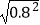 = ,
= , 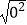 = ,
= , 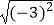 = ,
= , 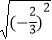 = ,
= ,
(2)根据计算结果,回答: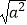 一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.
一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.
(3)利用你总结的规律,计算: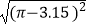 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.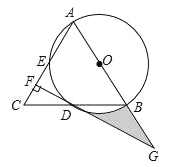
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )

A.2 B.3 C.4 D.5
相关试题

